What is a Number?

Introduction

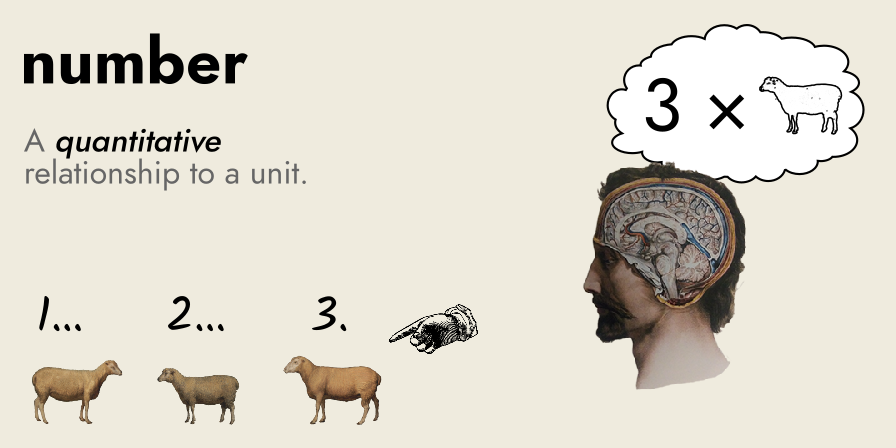
What exactly is a number? To me, it is one of the most fundamental questions in mathematics, but rarely have I found a good definition. The current Wikipedia article launches into a description of how numbers are used, without a succinct definition of what these things are, in themselves.^[1]

In school, I found it frustrating to spend so much time dealing with numbers, without knowing exactly what they were.

Are they real things? I mean, we were told about the “real” numbers, and worked with “imaginary” numbers—but why was one set of numbers called “real” and the other “imaginary”? Didn’t they both just exist in our heads?

Is zero a number? What about infinity?

It seemed absurd to study and work with numbers, yet not know exactly what they were.

In this article, I’ll be using the definition of numbers I encountered in “Mathematics is About the World”, by Robert E. Knapp.^[2] His treatment of numbers is top-class, demystifying the subject and laying it out clearly—a true reduction of the concept of number.

The qualitative and the quantitative

Relationships are ways of looking at the world, a comparison between things that can either qualitative or quantitative in nature, where:

• “Qualitative” refers to the nature of a thing, a characteristic feature or property. Either something has a given quality or it does not. A shape is either a circle or it is not, and so on.
• “Quantitative” refers to the amount of a given property, e.g. two men can have different heights, since “height” is a continuous property that allows a range of possible values.

No, relationships are not physically “real” like a rock—you cannot kick a relationship like you can kick a rock—but they have an objective existence, independent of opinion.

Qualitative relationships are a binary “yes” or “no” proposition. Either two men are brothers, or they are not—there is no in‐between.

Quantitative relationships refer to the relative amount of something. Two men might have similar heights, or one man may be much taller than the other.

The key difference is that quantitative relationships have a range of possible values, rather than the “yes”/ “no” nature of qualitative relationships.

We will see that quantitative relationships form the basis for numbers.

Quantitative judgements precede numbers

We make quantitative judgements that are not numerical all the time. We can easily tell if one man is taller than another man, or that one building is further away from us than another.

Even if we were totally innumerate, we could make such judgements—these sorts of quantitative comparisons are so primitive that animals can make them.^[3]

Anyone can compare a full basket of apples to a half-filled one and know that there are more apples in the full basket than the half-filled one. Even if they cannot say precisely how many more apples there are, they have an intuitive sense that one basket has more than the other.

When do quantitative judgements become numerical?

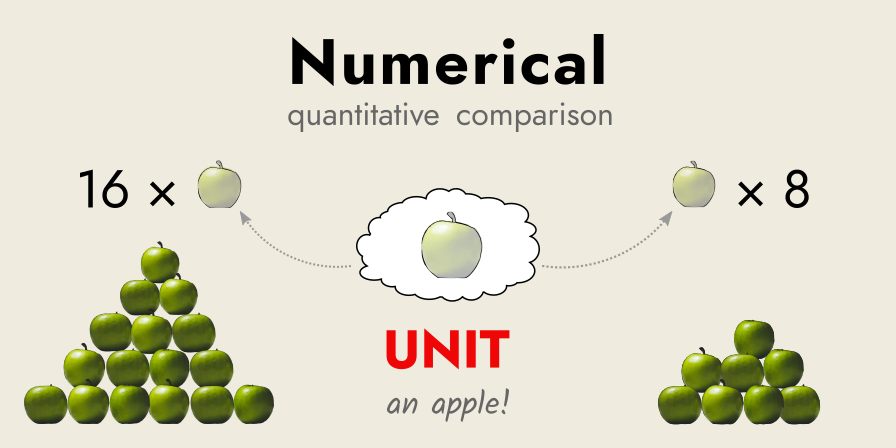
When we compare quantities precisely, using a chosen standard as a reference—this is where quantitative judgements become numerical.

Number, as a concept, reducts to finding the number of repetitions of our standard (e.g. an apple) that there is in the thing we are judging (e.g. a basket of apples).

The counting of multitudes

Where does the concept of “number” arise in the every-day world?

The fundamental act of counting is where number appears, and it builds from our inherent sense for quantity. When we count, we take a something as our standard (e.g. an apple) and compare it quantitatively to a group of similar things (e.g. a basket of apples).

The technical term for a group of individual things, like a crowd of people or a basket of apples is a “multitude”. A multitude is made up of distinct objects, and multitudes differ from properties like height and area, which are continuous.

Whether something is an “apple” or not is a qualitative property. For everything in the multitude (the basket of apples) we ask: is this thing an apple? If “yes”, we increase our count of apples by one; if “no”, we move onto the next thing in the basket without increasing the count.

The numbers we use to count are the whole numbers (0, 1, 2, 3…), and by “whole” we mean “not made of parts”. We use whole numbers to count distinct things, things that are separate from one another.

The quantitative relationship between our standard (the apple) and the multitude we are counting (the basket of apples) is the number. A number is a relationship, an objective relationship between unit and multitude, which specifies a quantity, the amount of repetitions of our standard in the multitude.

If we change our unit, we change the resulting number. Rather than a single apple, we could use a pair (two apples) as our standard—the count of “pairs of apples” will be different, despite the thing being counted (the basket of apples) remaining the same.

Measuring involves counting

When counting, we use a qualitative standard to determine the size of a multitude, and the count is the number of repetitions of our standard in the multitude, e.g. ten apples in the basket.

A magnitude is something like height and area, which is both quantitative and continuous. Can we count magnitudes the way we count multitudes?

No, we cannot.

Magnitudes and multitudes are fundamentally different.

Magnitudes are continuous, while multitudes are discontinuous (made up of individuals).

We count individual things, but in a magnitude there are no individual things to count—just a continuum!

So, what do we do?

We create a quantitative standard, from a magnitude of the same type, called a unit. This unit is then used to compare the size of magnitudes of the same type, by counting the number of repetitions of the unit in the magnitude. This process is called measurement.

An example: measuring a person’s height using a metre stick. The metre stick is our unit, and it clearly has a height of its own—and so it is a magnitude of the same type. Then, we count the number of times we can place the metre stick against the person: say two times, giving a height of two metres.

Yes, measurement involves counting, but it involves the counting of a unit against individual magnitudes, rather than increasing a count based on a qualitative comparison to a standard (as in the counting of multitudes).

Ratios compare magnitudes and multitudes

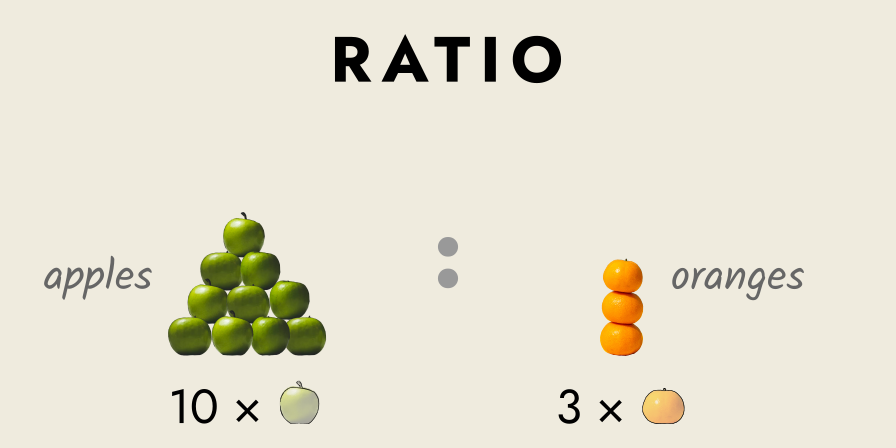
When measuring magnitudes we make a quantitative comparison between one magnitude (what we are measuring) and another magnitude (what we use to measure, our unit).

Any quantitative relation between things, where we focus on their relative size, is called a ratio. Ratios are written in the form 𝑎 : 𝑏, e.g. “10 apples : 3 oranges”, which is read as “10 apples to 3 oranges”, or whatever 𝑎 and 𝑏 are in each case.

Ratios involve comparisons between quantities, i.e. magnitudes or multitudes. An example would be the ratio of a man’s height to a two-foot ruler, say “6 ft : 2 ft”.

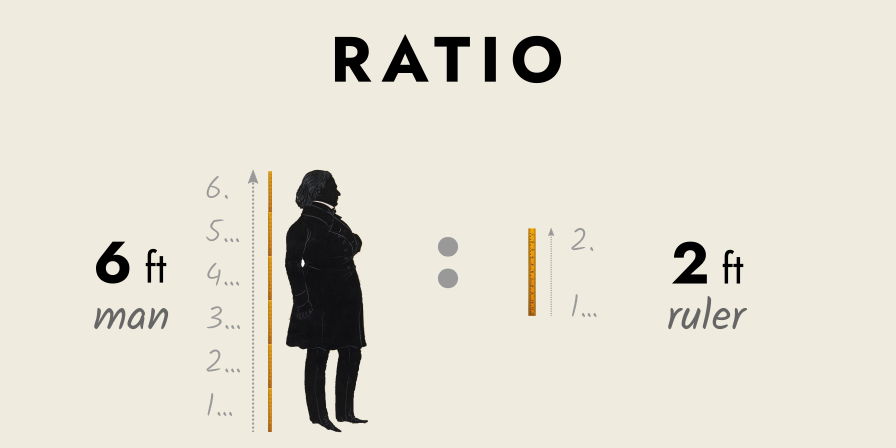
Unlike numbers, which are comparisons between two things (the unit and the thing being counted/measured), ratios can compare an unlimited number of things, e.g. “10 apples : 2 oranges : 6 lemons : …” and so on.

This means that only ratios between two things can result in a number, in the sense we are using here.

When a ratio can result in a number, this number is determined when the process of measurement (for magnitudes) or counting (for multitudes) is complete.

When counting, the process of is complete when we have tested every individual thing in a multitude against our standard, increasing our running total by one if the thing meets the standard, i.e. “Yes, this is an apple, add ‘1’ to the total.” etc.

And when is a measurement complete?

Measurement is complete when we “count off” the number of times the unit (e.g. a ruler) is contained in the magnitude being measured (e.g. the man’s height). Then, we record a number that describes the quantitative relationship between the magnitude and our unit.

But most of the time, a magnitude cannot be counted with whole numbers, like the individuals in a multitude can. A man’s height might not be five feet or six feet exactly, but something in-between.

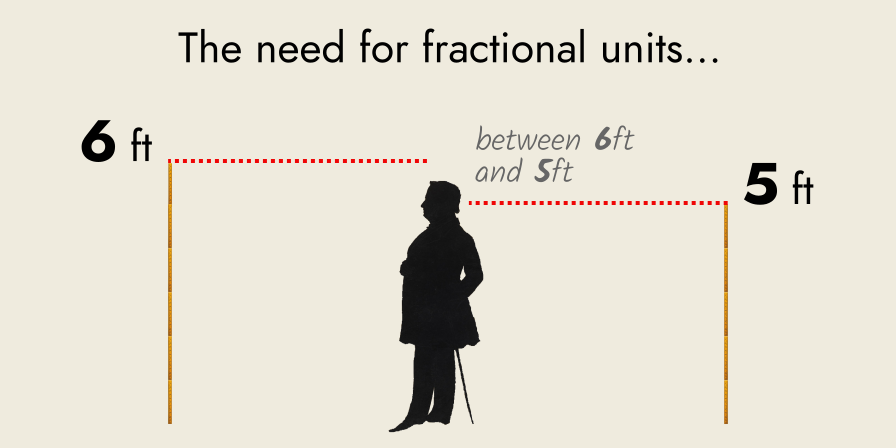
In such cases, whole numbers are inadequate for measurement: they count complete, individual things, and height has a continuous range of values.

What to do?

Rational numbers and fractions

Since magnitudes can have a range of values, which lie in-between our whole numbers (1, 2, 3…), we need to divide up our whole numbers into smaller parts, allowing us to “cover” more values.

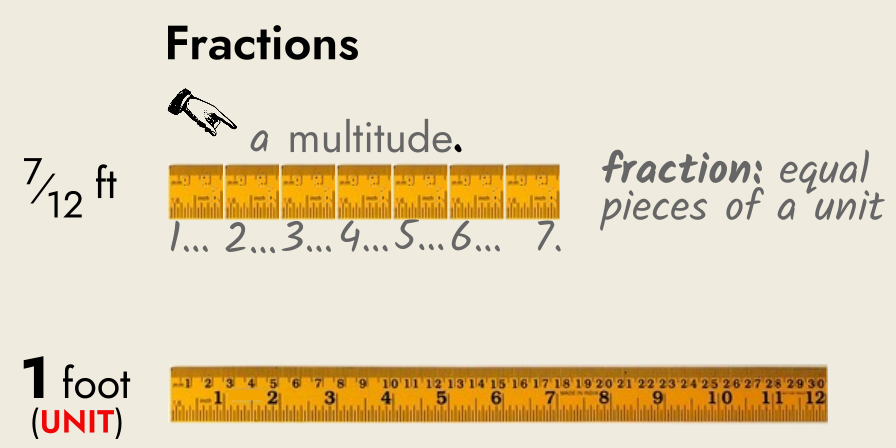
We introduce fractions, equally‐sized sub‐divisions of our original unit: one foot (ft) is divided into twelve inches, where one inch (in.) can be written as the fraction ¹⁄₁₂ ft, two inches as ²⁄₁₂ ft etc.

Now, using a combination of feet and inches, we can “count off” the man’s height: we find he is 5 ft 7 in. tall, read aloud as “five‐feet, seven‐inches”. This measurement can be written entirely in terms of feet, as 5 ⁷⁄₁₂ ft.

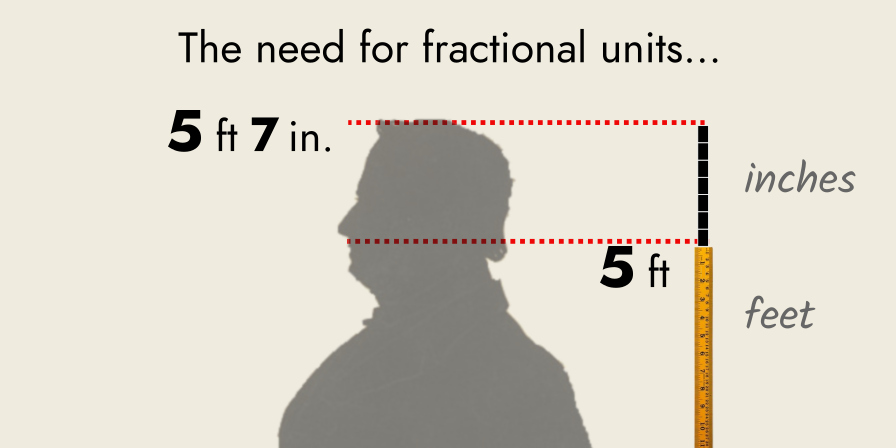
The “5 ⁷⁄₁₂” here is a new type of a number, a rational number: a comparison between whole numbers that allows us to count the (possibly fractional) number of units in a magnitude.

Note, the format of “5 ⁷⁄₁₂” is called a “mixed number”, since it is a mixture of units (feet and inches). This is the traditional way that measurements were recorded; modern scientific measurement tends to use decimal notation.

The height of 5 ⁷⁄₁₂ ft can be written completely in terms of inches i.e. ⁶⁷⁄₁₂ ft, in what is called an “improper fraction” (since the top‐part is larger than the bottom‐part).

Generally, rational numbers are written in the form of fractions, i.e. ^𝑝 ⁄_𝑞, where 𝑝 and 𝑞 are whole numbers, and 𝑞 is not zero. Importantly, this does not mean that rational numbers are fractions, merely that rational numbers can be expressed in fractional format.

For example, the rational number represented by the fraction ⁷⁄₁₂, can be written in decimal format as 0.583, where the bar over the numeral “3” is called a vinculum, and means the numeral is repeated forever.

I think of fractions as literal sub‐divisions of a unit, as individual pieces of a larger unit. If you have seven inches, you have seven sub‐divisions of a foot, with each sub‐division being ¹⁄₁₂ th of a foot. That is, fractions are multitudes (groups of things).

On the other hand, rational numbers describe quantitative relationships between things—they are not multitudes like fractions are, nor are they magnitudes like lengths are.

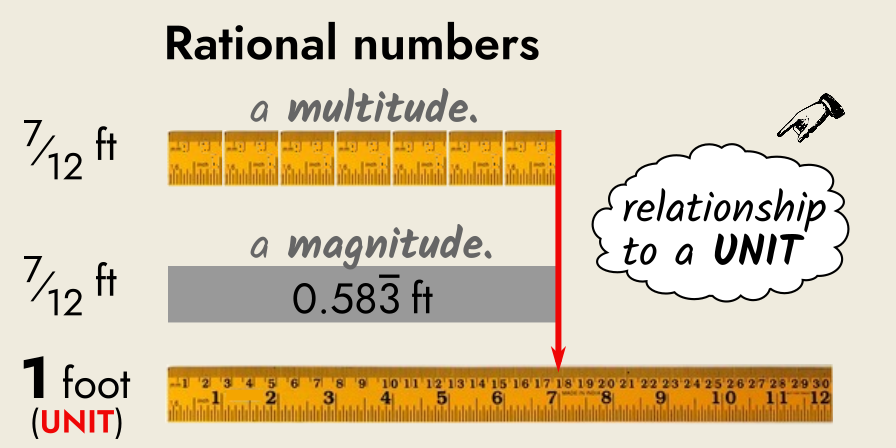
Confusingly enough, the fractional format of ^𝑝 ⁄_𝑞 can also be used to represent magnitudes, like a continuous length.

Rather than seven separate inches lined up together, we could have a short length written in fractional format as ⁷⁄₁₂ ft. The same short length is represented in decimal format as 0.583 ft.
(I have a few thoughts on this “flexible” use of fractional notation, which I’ll share another day.)

Thus, rational numbers describe both multitudes and magnitudes, and regardless of the specific format—fractional or decimal—they remain a rational number, a comparison between whole numbers.

Note, the word rational is not derived from the word ratio, despite their similarity and related nature. In this case, rational means “not irrational”. The term irrational (regards numbers) comes via Latin, from a Greek word, alogos, which literally means an unsayable or unreasonable number.^[4]

In a mathematical context, “irrational” refers to a number that cannot be completely specified—its exact value can never be fully known, in contrast to rational numbers, which can be completely specified as a ratio between whole numbers. We’ll cover irrational numbers in more depth shortly.

Negative numbers

We’ve seen how numbers represent a quantitative relationship between multitudes and the standard used to count them, or between magnitudes and the units that measure them.

In the physical world, multitudes and magnitudes are never less than zero, i.e. they are never “negative”, always “positive”. This is true for the whole numbers used for counting, and for the rational numbers used for measuring.

If a shepherd loses his entire flock to wolves, he will have zero sheep—and not a negative amount. What would a negative sheep even look like? An abhorrent vacuum in the shape of a woolly ruminant?

What can be negative however, is the difference between two multitudes (or magnitudes).

For example, comparing two barrels of apples, we find that the first barrel has 100 apples and the second 75, in which case the difference between the first and the second is 25 (100 − 75), since the first barrel has more apples.

But we can just as easily look at things from the perspective of the second barrel, where the difference is −25 (75 − 100), since the second barrel has less apples than the first.

When comparing things quantitatively, negative numbers can be conceived of as “opposite” in some way, or to indicate the lack of something.

If your bank account becomes overdrawn, it means your balance is less than zero. This does not mean that there is a money-shaped void sitting in a bank vault somewhere: it just means you owe money.

The concept of “negative” introduces a qualitative aspect to numbers, which were purely quantitative to begin with. The numbers 5 and −5 are both the same size, just with an opposite character—the physical interpretation of this opposite characteristic will vary depending on the situation.

Combining the whole numbers (0, 1, 2, 3…) and their negative counterparts (−1, −2, −3…) gives us a new group of numbers called the “integers”; the integers are included in the rational numbers (along with positive and negative fractions).

Irrational numbers

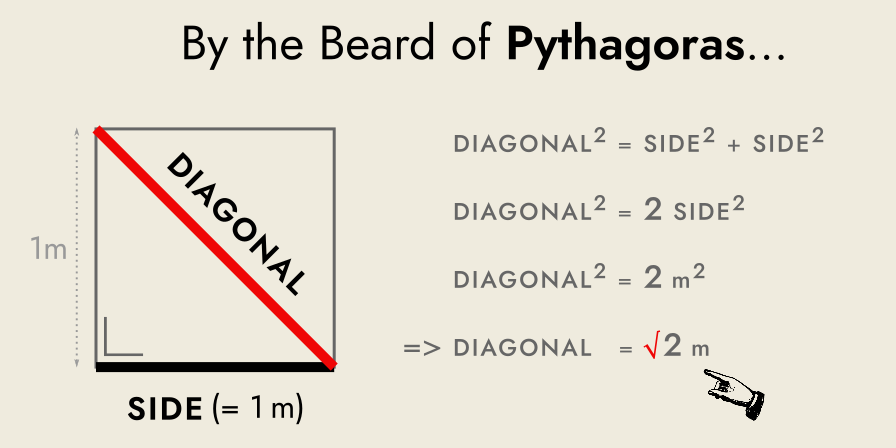
Consider a “unit square”, built from a side exactly one metre long, where “unit square” just means that the side of the square is exactly one unit long. We’ll use one metre as our unit in this example. On this square, we draw a diagonal line from one corner to another.

In terms of our unit (the side), what is the length of the diagonal?

By the Theorem of Pythagoras, we know that: diagonal ² = side ² + side ²

So in this case, the diagonal is the square root of 2 metres long, written as √2 m.

What is the exact value of √2?

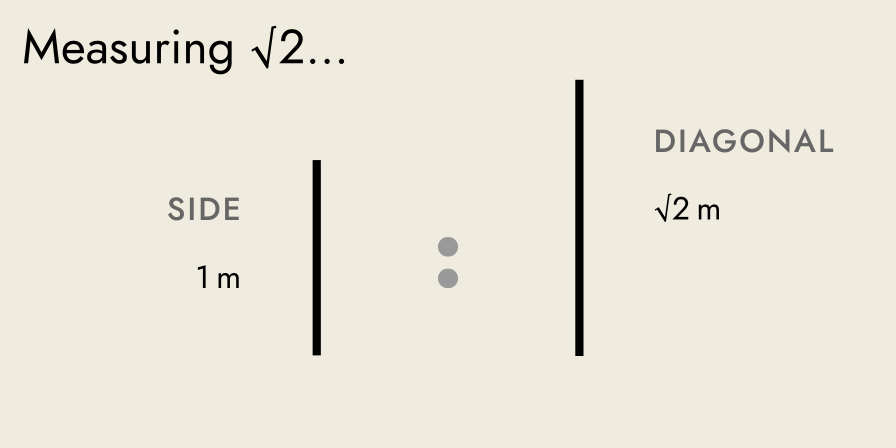
To find the value of √2, and to illustrate the concept of irrational numbers, we’ll pretend the following three measurements have been made, of the same square, using progressively smaller units:

• A carpenter uses a metre stick, and measures the side as 1 m exactly. He finds the diagonal to be 1.414… m, a fractional number that he cannot measure exactly.

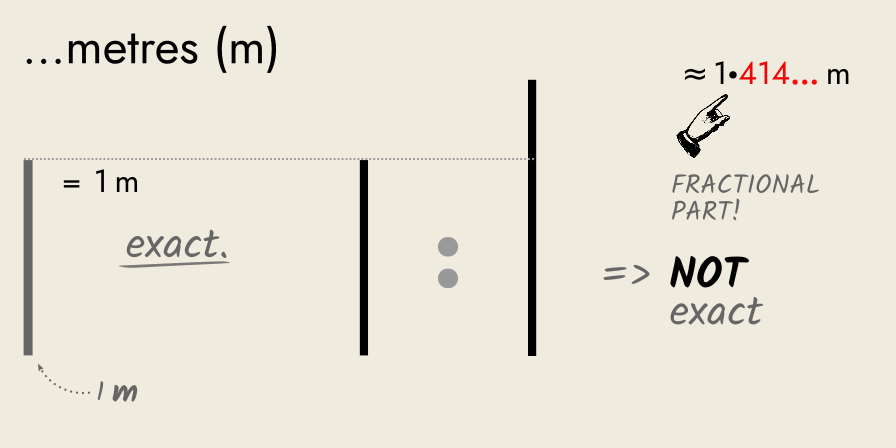
  So, we need a smaller unit to try and measure it exactly.

  ---

• An engineer uses a millimetre (a thousand of a metre) and measures the side as 1,000 millimetres exactly. She finds the diagonal to be 1,414.213… millimetres, a fractional number that she cannot measure exactly.

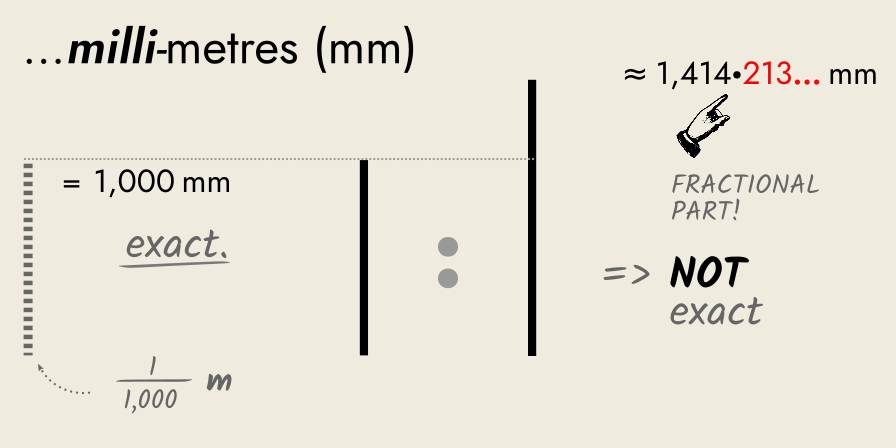
  So, we need a smaller unit to try and measure it exactly.

  ---

• A physicist uses a micrometre (a millionth of a metre) and measures the side as 1,000,000 micrometres exactly. He finds the diagonal to be 1,414,213.562… micrometres, a fractional number that he cannot measure exactly.

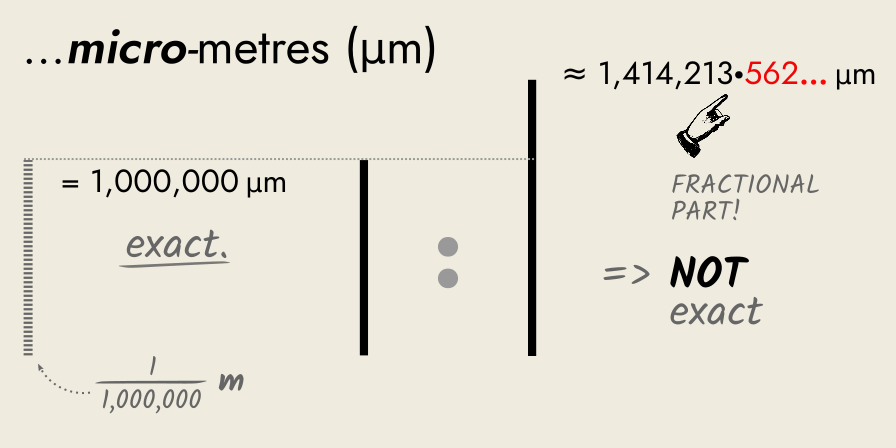
  So, we need a smaller unit to try and measure it exactly.

  ---

Can this game go on forever?

Yes, yes it can.

At least in the abstract world of mathematics that is. In the real world, we are always limited in our precision, and eventually there are units so small that we cannot see the fractional parts.

In mathematics however, we are not limited by our eyeballs or tiny units—only our imagination.

In an abstract setting, the ratio of “DIAGONAL : SIDE” is not something we can express as a fraction of two whole numbers—it cannot be written as a rational number, only approximated by one.

The number we have labelled as √2, and all numbers like it, are called irrational numbers. We can specify them to a million, billion decimal places, but we can never express them completely.

Thus, the side and the diagonal of a square are incommensurable: they cannot be compared to one another in terms of a rational number, a ratio of whole numbers. That is, there is no smallest unit that will fit into both lengths a whole number of times: there will forever be a fractional part to √2, no matter how small the unit is.

It might seem weird and surprising that we can construct lines that we cannot completely measure in terms of each other—but that is because it is weird and surprising. It was a discovery of the ancient Greeks, who were the first to study “incommensurable magnitudes” (i.e. irrational numbers) systematically, considering them separately from the rational numbers.^[5]

To ward off any mystical notions that might be developing, let me state that there is nothing “irrational” or mysterious about the diagonal itself—it is a line segment with a finite length, just like any other. The irrationality arises when we try to measure the diagonal in terms of the side: it is the method of comparison that produces the irrationality, not the things themselves.

Grouping the rationals and irrationals together gives us a new set of numbers called the real numbers. The term “real” (French: réelles) was first used by Rene Descartes to distinguish these numbers from the “imaginary” numbers (French: imaginaires),^[6] which we will discuss next.

Imaginary units and complex numbers

That this subject [imaginary numbers] has hitherto been surrounded by mysterious obscurity, is to be attributed largely to an ill adapted notation.

If, for example, +1, −1, and the square root of −1 had been called direct, inverse and lateral units, instead of positive, negative and imaginary (or even impossible), such an obscurity would have been out of the question.

Consider the following simple equation: 𝑥² + 1 = 0Solving for 𝑥 gives us the following strange result: 𝑥 = ±√−1

What is this bizarre number, √−1, the square root of −1?

There is no real number that when squared gives −1, so what is it?

Is it even a number?

Surprisingly, yes it is a number: its name is the “imaginary unit” and its symbol is 𝑖. Starting in 16^th century Italy, this mysterious number has been used extensively by mathematicians to solve challenging equations.^[7]

That said, while 𝑖 has always been useful, many were unsure of what exactly it was: Gauss stated as late as 1825 that “the true metaphysics of the square root of −1 is elusive”.^[8]

Eventually, a simple physical interpretation of the imaginary unit was developed: turning sideways!

Imagine (no pun intended) you are facing East.

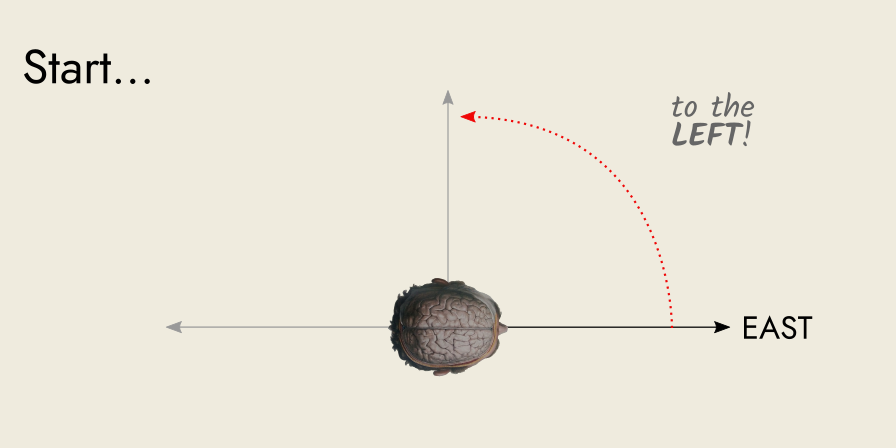
You turn 90° to your left. You are now facing North.

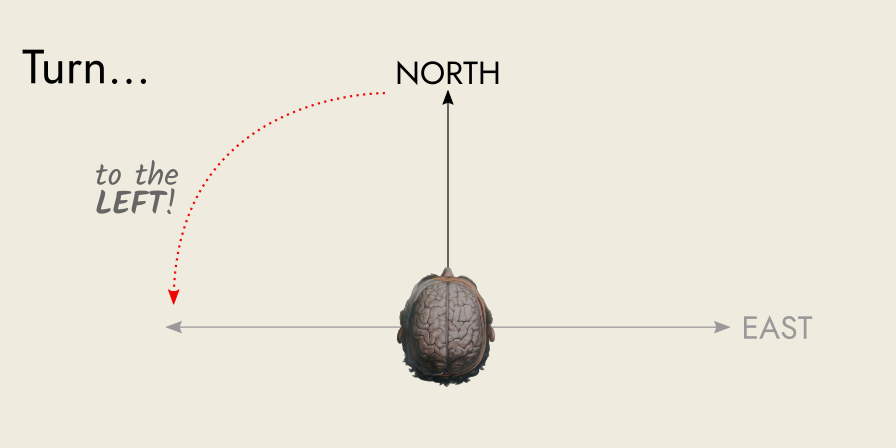
Then, you turn another 90° to your left, and you are now facing West: the opposite direction to East (where you were facing, initially).

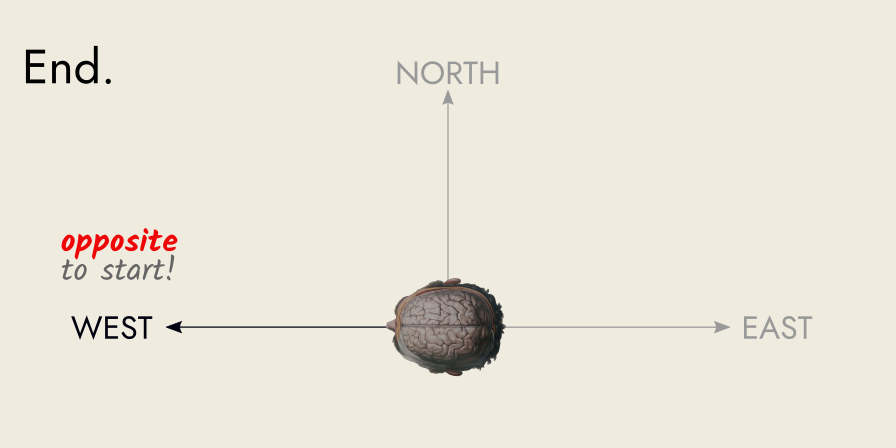
The physical act of turning sideways twice, results in you facing the opposite direction in which you started.

Nothing mysterious here you say? Well, no, there isn’t—but this simple physical action helped kick the mystery out of imaginary numbers, by giving them a direct physical referent.

Now, we can interpret multiplication by 𝑖 as an anti-clockwise rotation of 90° from the direction we are facing. If we interpret “+1” as facing East, then multiplying by 𝑖 twice ( 𝑖² ) gives us “−1”, which we interpret as facing West.

Thus, the “imaginary unit”, 𝑖, can be interpreted as a rotation of 90° anti‐clockwise (to the left) from a reference point. An equal turn in the opposite direction, i.e. a rotation of 90° clockwise (to the right) from the same reference point, is labelled −𝑖.

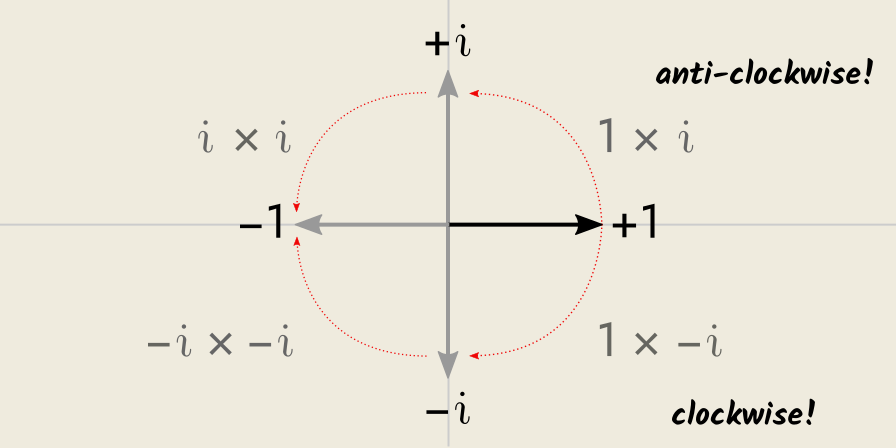
We can create a new class of numbers, the complex numbers, by combining the reals and the imaginary unit. Complex numbers have the following form: 𝑎 + 𝑏 𝑖, where 𝑎 and 𝑏 are reals.

Using complex numbers, we can build a new co‐ordinate plane, with the real numbers providing the horizontal axis (left‐to‐right), and the imaginary numbers providing the vertical axis (up‐and‐down).

Complex numbers are quite literally number extended to another (abstract) dimension: from the one-dimensional real number line to the two-dimensional complex plane.

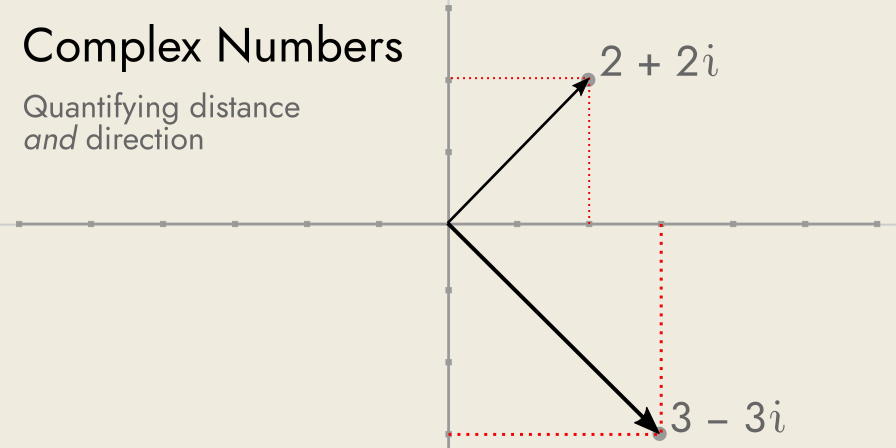
While negative (real) numbers could only represent “opposite in direction”, complex numbers provide the ability to fully quantify direction, as well as magnitude. This makes them incredibly useful for the modeling of vectors, which are magnitudes associated with a particular direction, e.g. velocity, force etc.∎