Infinite Angels, Dancing on a Pinpoint

Lines versus line segments

Firstly, a line is an infinite length.

A line is an abstraction (an idea in the mind), where we focus only on the length of the thing, and ignore its width.

You can never draw a line in its entirety, only a part of it.

Lines are made up of infinite number of points, since a line itself is infinite. No issues with that.

But, what about line segments?

A line segment is a finite length.

Any “line” you draw with two visible end-points is a line segment, e.g. the side of a shape etc.

How many points are there in a line segment?

Commonly, people claim (see below) that there is an infinite number of points in a finite line segment.

But I think this claim is ill-conceived and contradictory.

Can the finite be made up of the infinite?

Can a finite line segment made up of an infinite number of dimensionless points?

Sound like a silly question that only pedants would debate?

Perhaps.

But if you have studied mathematics, then you will have encountered this notion.

As mentioned, people claim that line segments have an “infinite number of dimensionless points”.

(And by “dimensionless”, we mean “no length, breadth or depth”. That is, they take up no space whatsoever.)

I think this notion is blatantly self-contradictory and damned confusing.

And I’ll show you how it contradicts itself, using an old theological question as a starting-point.

Firstly, an important point about “points”.

What’s the point of points?

Google “What is a point in mathematics?” and you’ll get results claiming, variously:

• that a point has “only position”, and
• it does NOT have length, width or breadth.
• It is dimensionless (allegedly) and takes up no space.

Sound confusing and contradictory?

Certainly does to me.

I recall every time a teacher wanted to represent a “point” on the blackboard, they would draw a dot.

A mark of chalk with a definite length, width and breadth.

Then they would claim a point has NO length, width or breadth.

(Despite just drawing it with a damned length, width and breadth!)

E-gad, the non-sense of this!

It’s like the Invisible Pink Unicorn.

Both invisible and pink.

Baloney.

I’ll use a more sensible definition of a “point” for this article: the smallest part of a line, which we can separate from all other parts of the same line.

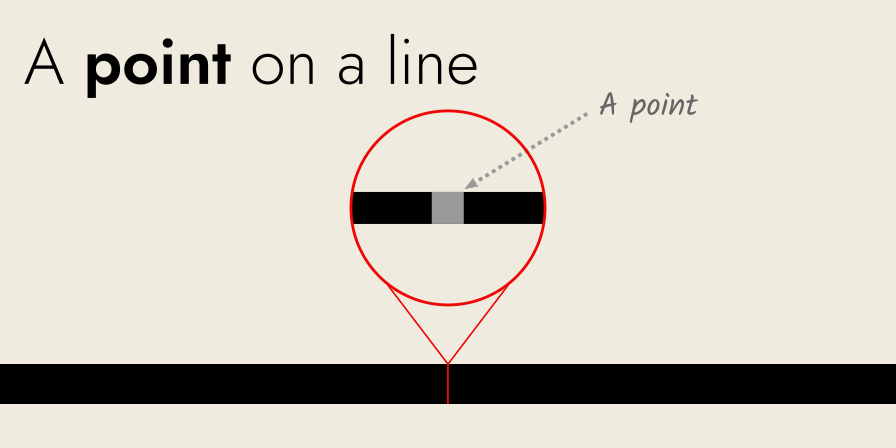
The unaided human eye can see down to about a millimeter.

So for an unaided human eye, a “point” of a line is a millimeter length.

In my definition, a point takes up space.

It is not some fantastical, spiritual entity that both exists, yet takes up no space.

How many angels can dance on the point of a pin?

If you are an English speaker (by choice or by chance), you may have heard of the theological question: “How many angels can dance on the point of a pin?”.

(Or, “How many angels can dance on the head of a pin?”)

This phrase is used figuratively to suggest a question is of no value.

That asking the question is pointless, irrelevant and a waste of time (regardless of your belief in angels).

The phrase was originally used by writers of the Modern Era (1500s onward) to disparage and ridicule the (Catholic) medieval scholastics, by claiming they wasted time debating pointless questions.

(The medieval scholastics were neither fools nor time-wasters. They laid the groundwork for modern science, which I will show in a future article.)

I’m going to show how this supposedly “useless” question is actually very relevant and informative, when considering the nature of points and line segments.

The spiritual and the physical, in terms of space occupied

The key aspect of the question “How many angels can dance on the point of a pin?” relates to the nature of angels (if they exist, of course).

Specifically, are angels corporeal entities?

“Corporeal” means physical beings that take up space. That is, physical things that have spatial dimensions. Like humans.

Or, are angels non-corporeal entities?

“Non-corporeal” means non-physical beings (spirits) that do NOT take up any space at all. That is, spirits are dimensionless, taking up no space whatsoever.

If angels are corporeal (physical), then you can only fit so many of them in given place, no matter how tiny they are.

If angels are non-corporeal, then you can fit as many as you want in any given place.

Non-corporeal entities are dimensionless and can be stacked on top of each other indefinitely.

Staring at pinpoints, looking for angels

Assume the point of a pin (a pinpoint) is the smallest place a human can perceive. If angels were smaller than a pinpoint, humans could not see them.

So, we assume that an angel is at least as big as a pinpoint.

If angels are corporeal and take up space, you can fit only one of them on a pinpoint.

Two angels cannot occupy the same space (at the same time), any more than humans can.

There is only space on a pinpoint for one angel, since an angel is just big enough to occupy a pinpoint.

If angels were smaller than a pinpoint, we couldn’t see them, remember? (Since the smallest thing we can perceive is a pinpoint).

Now, let’s consider the opposite case.

Let’s assume angels are non-corporeal (spirits), that they take up no physical space whatsoever.

They are “dimensionless” in other words.

So, they have no length, breadth or depth. They do NOT extend in space.

If angels are non-corporeal and do not take up any space, then you can fit as many as you like on a pinpoint.

If an angel does not take up any space, then one…ten…a million…a billion…an infinite amount of non-corporeal angels can dance on the point of a pin!

When old theology meets modern mathematics

How do dancing angels relate to line segments?

Consider the angels to be “points” on a line segment, the smallest thing we can conceive of.

Are these points corporeal (they take up space) or non-corporeal (they do NOT take up space)?

If points take up space (no matter how small that space is), then you can only fit so many together in a finite length.

A point cannot occupy the same space as another point, no more than a person can occupy the same space as another person (at the same time).

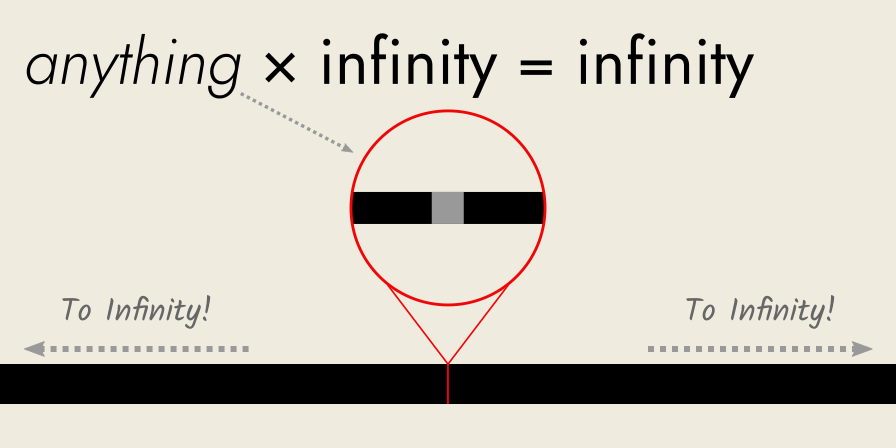
If points take up physical space, then you cannot have an infinite number of them in a line segment.

Why not?

Because an infinite number of points would result in an infinite line—and not a finite line segment.

On the other hand, if points are non-corporeal and do NOT take up any space, then you can fit as many as you like in a given place.

You can fit one…ten…a million…a billion…an infinite amount of non-corporeal points into the same place!

And so, you would have no length at all.

You would be just adding nothing to nothing, which is always just nothing.

(Since these points have no physical length, at all).

When Mathematicians Contradict Themselves

The following is the full text of a post from Math StackExchange, from a mathematician trying to explain how a finite line segment could made up of an infinite number of points:

The concept of infinity is used for many different things, and one should not confuse them. A line, be it closed, open, straight, curved, finite in length, or infinite in length always consists of infinitely many individual points (at least for any reasonable notion of ‘line’).

This can be proven rigorously, and it’s not hard at all. Basically, between any two distinct points on a line there is a third point between these two points (between should not necessarily mean the mid-point on a straight path connecting the points, and this may get a bit tricky, but not too tricky).

The length of the line is a different issue. It may be finite in length or infinite in length. The totality of the points comprising the line is in any case infinite.

In fact it can be shown (quite easily) that the cardinality of points of any line is always the same, so in a sense all lines have the same “amount” of points in them, though the way these points are arranged may give totally different geometric qualities to the line.

No offense to Mr. Weiss, who means well and gives the standard explanation, but his explanation misses the mark.

Why?

Because the word “point” varies between the common, everyday usage and the specialist mathematical usage.

There is a big difference between the physical parts that make up a line, and the points we can mark on that line.

Simply stated, a “point” means either:

• common usage: a part of a thing; a concrete thing with physical extension.
• mathematical usage: marks an exact location in space; an abstraction without physical extension.

The two concepts are very different, but mathematicians often forget that the common notion of “point” conflicts with their precise definition.

And thus, the mathematical explanation of points and line segments can seem confused and contradictory to the non-mathematician, who has a very different notion of what a “point” is.

Conflating the two throws forth a horde of confused notions, like the idea that all line segments (of different lengths) have the same number of parts.

How can any line segment be any different than any other, if they all have the same number of parts!?

Yes, you can mark an infinite number of points on a meter stick, in theory at least: 0.8… 0.87… 0.874… 0.875…

All these points could be marked on a given meter stick—in principle, if not practically.

But, these hypothetical marks do not constitute the meter stick itself.

The marks we make (on the meter stick) are not the “stuff” that make up a meter stick. They are a secondary thing, without substance, an artifact of measurement.

The “stuff” of the meter stick relates to what we call “geometric magnitude”, which means the “space” taken up by something.

A thing is “made up” of its parts, and a larger stick has a greater magnitude than a shorter one, since it has more parts (of the same size) than the smaller one.

That we can make an infinite number of marks on either stick is irrelevant to the number of parts they each contain.

When we mark a line, the marks we make describe the line—they do not “make up” the line.

The common notion is confused and contradictory

Mr Weiss is not alone in his conceptions.

In fact, his views are typical.

I googled the phrase “a line segment is made up of an infinite number of points”.

The top result on Google was from a site Toppr.com, which is typical of what is said:

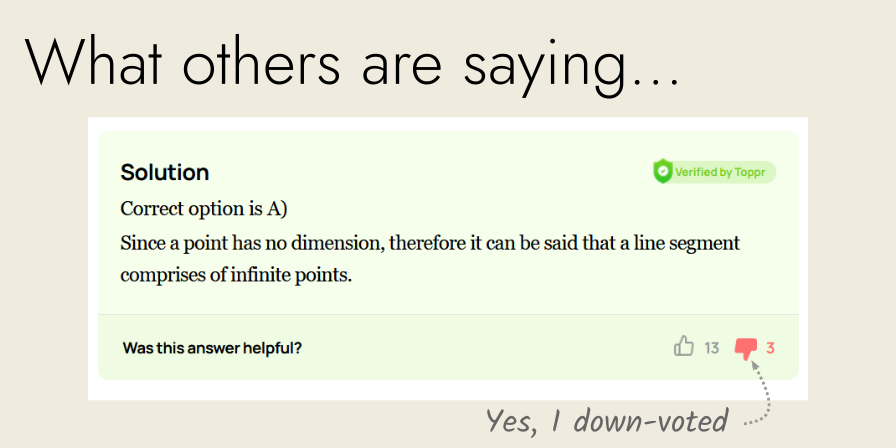
This is contradictory non-sense, which is repeated by the other posters over at Math StackExchange.

Setting things straight

If your points take up space (no matter how small).
And if you have an infinite amount of them.
Then you will have an infinite line.

(An infinite amount of anything is infinite.)

If your points take up NO space.
And if you have an infinite number of them.
Then you will have nothing at all.

(An infinite amount of nothing, is still nothing.)

So, what are line segments made up of?

What are line segments made of?

We’ve just proven that line segments can NOT be made up of an infinite number of points.

This assumption must be rejected since it leads to either:

• an infinite line (if the points extend in space), or
• nothing at all (if the points do not extend in space).

Therefore, line segments must be made up of a finite number of points, where each point has an extension in space.

Each point must have an extension in space, because otherwise we get nothing (as we saw above.)

And there must be a finite number of points.

Why?

Because an infinite number of points (that extend in space), gives an infinite line (rather than a finite line segment).

But, how many points are there in a given line segment?

Excellent question!

A new type of number is needed

The question “How many points are there in a given line segment?” has an answer, but it requires an unusual type of number.

A type of number that is rarely taught in modern schools.

These numbers flirt with the infinite, and have invited controversy down through the ages.

But these numbers have a long history of use by mathematicians, scientists and engineers.

Archimedes used them to figure out the equation for the volume of a sphere (over 2,000 years ago!).

Newton and Leibniz used them when developing our modern calculus.

These numbers are the infinitesimals.

And, in a future article, I will show how they can be used to sensibly describe the quantitative relationship of points to line segments.

(Without any of the contradictory waffle we saw previously.)∎