Indefinite Numbers: Infinitesimals without Infinity

Introduction

In a previous article, I claimed infinitesimals were a new type of number.

One that flirted with the infinite.

I claimed they’d resolve the paradox of finite line segments being be made up of infinite parts.

Interested?

They are an intuitive and brilliant concept, and have delivered some of the greatest discoveries in mathematical history (e.g. the area of the circle, calculus).

Despite this, they have been shunned by some mathematicians on grounds of logical “rigor”.

I won’t bore you with the details, but until very recently, infinitesimals were on “shaky ground” (from a formal perspective).

Thankfully, the work of Abraham Robinson on “Non-Standard Analysis” (in the 1960s), has placed the concept of infinitesimal quantities on a “rigorous” footing.^[1]

Hopefully, this will appease the pedantic and see infinitesimals taught more widely.

That said, Robinson’s infinitesimals are built on the concept of infinitely small (and large) quantities. And this notion of infinitely small (or large) things is something I find nonsensical.

So, I’m going to introduce a type of infinitesimal, one built on incomprehensibly small (but still finite) quantities.

Here, I’ll introduce the finite infinitesimals and their inverses, the finite unlimited numbers, and (in future articles) show how they can be used to:

• find the area of curved shapes, e.g. circles
• simplify calculus, and
• make sense of the relationship between points, parts and line segments.

I’m going to call these new numbers the indefinite numbers, since they are going to be as small (or as big) as you need them to be.

Infinitesimals as infinitely small quantities

Infinitesimals are often defined as a number that is smaller than any finite number, but still greater than zero.

The word “infinitesimal” is formed from the Latin for “infinity” (infinitus) and the ordinal position indicator (-esimus).

Literally, it means “infinity-eth” (like 4ᵗʰ, 5ᵗʰ…) and should be interpreted in the sense of a fraction, i.e. less than one.

Smaller than anything, but not nothing.

That is, infinitesimals are “infinitely small” (according to this definition).

I don’t like this definition.

The concept of infinitely small or large quantities makes no sense.

Infinity is a place you can never reach.

Like trying to chase a rainbow.

It will be forever beyond you, always out of reach.

To claim that a quantity, 𝑥, is infinitely small (or large), implies that you have measured it and determined its size.

This is how we measure things, both in the real-world and in the abstract world of mathematics.

We take a unit and compare our unit to the thing being measured, in terms of quantity.

There are 5,280 feet in a mile.

The diagonal of a square is √2 times its side.

And so on.

Before we can declare the size of something, the measurement process (the counting of units) must have ended.

But how can you declare something “infinite”, when you can never reach infinity (by counting off units)?

Infinite quantities by fiat

How do mathematicians resolve this conundrum?

The reaching of an endpoint that cannot (by definition) be reached?

Simple.

They declare: “Let there be infinite quantities!”

And there are infinite quantities.

As Lords of their own formal universes, they have every right to declare such things.

And provided this decision avoids logical contradictions i.e. it is consistent, they can happily work with these new quantities, studying their properties (even if they don’t make intuitive sense to most people).

And that is what Abraham Robinson did with Non-Standard Analysis.

So, let us discuss Non-Standard Analysis, since it provides some brilliant ideas, which I will later borrow for my own purposes.

The concept of the hyper-reals

There are no infinite numbers, large or small, among the real numbers (denoted by 𝐑).

All real numbers are finite, no matter how large or small they are.

To recap, the real numbers are made up of the:

• rational numbers

  Finite numbers that can be fully specified. Usually written as a ratio of two whole numbers, e.g. 1, 3/2, -10/9 etc. We can use decimal format to describe them as well, e.g. 1, 1.5, 1.111 (where the bar indicates the pattern continues forever).

• irrational numbers

  Finite numbers that cannot be fully specified. Since we can only approximate them using rational numbers, we use special symbols like √2 and π, to identify these numbers. The number given by √2 has a value of:1.41421…

  The ellipsis, …, indicates an infinite sequence of digits with no pattern.
  (Note, the sequence describing the number is infinite, not the number itself.)

  ---

Thus, the concept of “infinitely” small or large doesn’t belong among the real numbers.

All real numbers are finite.

Which is why Abraham Robinson had to extend the reals to include infinite quantities.

He created a larger set of numbers: the hyper-real number system, denoted as *𝐑.

We started with the natural numbers (0,1,2, 3…) for ordinary counting.

Then, we found situations where the natural numbers were not enough.

And so we expanded the concept of number to include negative numbers, fractions, and irrationals etc.

Robinson did the same with the real numbers.

He added to them numbers that are infinitely small (infinitesimal hyper-reals) and infinitely large (infinite hyper-reals).

His work showed that these hyper-reals are logically consistent with the behavior of the real numbers.

So, the basic operations you can do with real numbers (arithmetic, trigonometry etc.), you can do with the hyper-reals.

The details are very academic and high-falutin’, so I won’t discuss their foundations any further.

(All beyond me anyways!)

Instead, let’s talk about the hyper-real numbers themselves, in more detail.

Some aspects of the hyper-reals

The complex numbers, e.g. 2 + 3𝑖, are formed from a real number, i.e. 2, and an imaginary number, i.e. 3𝑖.

Similarly, a hyper-real number is formed from a finite part and an infinite part.

It is a compound number, composed of two different types of number: one of them familiar and the other foreign to everyday experience.

The finite number is called the standard part, and the infinite number is called the non-standard part of the hyper-real number.

Hence, “Non-Standard Analysis”.

A simple example of a hyper-real number would be this: 5 + 2𝜔

What is this 𝜔 (a lower case omega)?

It is the first infinite number in Robinson’s system.

This number, 𝜔, is greater than any real number.

That is, for any finite sum of integers: 1 + 1 + 1 + … < 𝜔

It cannot be constructed from the real numbers: it is in a “class” of its own. (If this notion of an “infinite” number seems a bit strange to you, fear not—I agree!)

If you take a yard stick, and divide it by a million, you will get a million little pieces.

And each piece will be one millionth of a yard in size.

That is, if you divide a thing by a large number, you will get a large number of tiny pieces.

So, if:

• we take one unit (whatever unit you please), and
• divide it by 𝜔, we get
• an infinite number of pieces, with each of those pieces being infinitely small.

Where 𝜔 was infinitely large, each of these pieces is infinitely small.

These pieces represent the first infinitesimal hyper-real number, denoted 𝜀 (lower case epsilon).

In mathematical jargon, the infinitesimal number 𝜀 is the reciprocal of the infinite number 𝜔.

A “reciprocal” means the number that results, when you divide the number one by a particular number.

That is: 𝜀 = 1/𝜔

An infinitesimal number, 𝜀, is less than any real number.

Namely, for any positive real number, 𝑛: 0 < 𝜀 < 𝑛

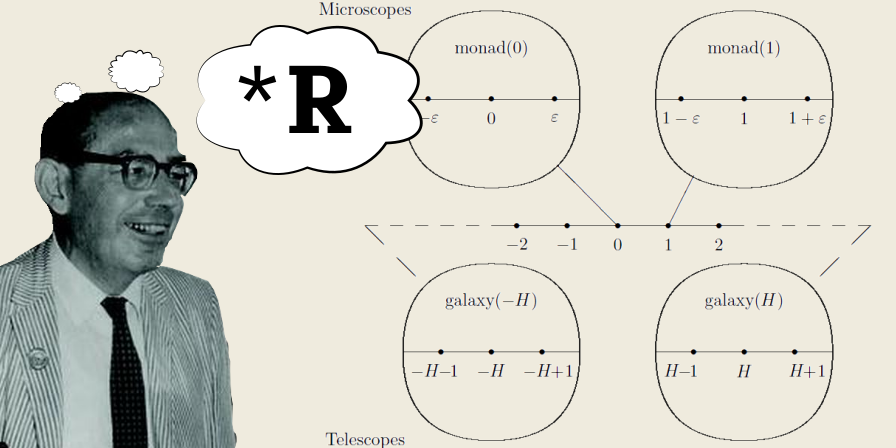
In Robinson’s scheme, all real numbers are surrounded by a cloud (or halo) of infinitesimal hyper-reals.

Numbers that are both infinitely small and infinitely close to the real number.

Like a garland of guardian angels around every one of the real numbers.

Building on Non-Standard Analysis, the mathematician K. D. Stroyan formally described the “magnification” of a function in 1972.^[2]

This concept was given a graphical treatment by Jerome Keisler in 1976, providing an intuitive notion of “zooming” in-and-out on a graph.^[3]

Imagine you have an infinitesimal microscope.

This microscope has the magic ability to zoom to an infinite degree—making infinitesimals visible from our (initially) finite perspective.

By zooming in on a point on the real number line, e.g. “1”, we can see the halo of infinitesimals that surround it—something we cannot see from our regular, finite perspective.

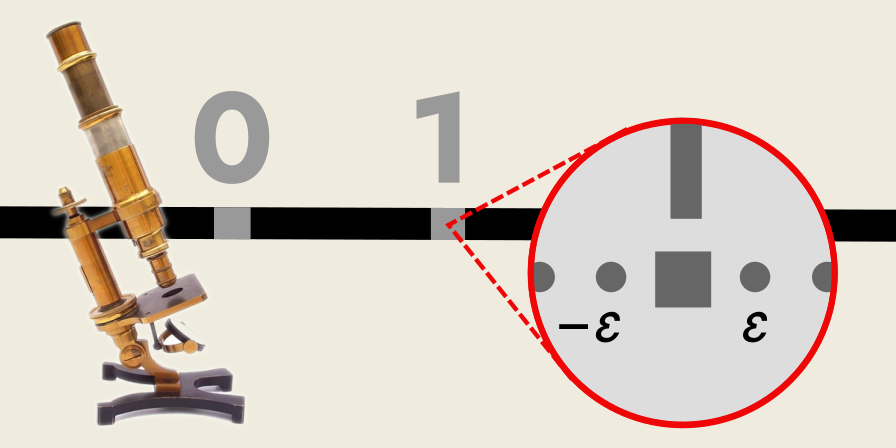
From our standard perspective, we cannot see these infinitesimals without our microscope.

They are beneath our perception.

(But they are there, none-the-less.)

Similarly, the infinite hyper-reals cannot be seen from the standard perspective.

Like far-away galaxies, they are beyond our perception—too far away to be seen.

So, we use an infinite telescope, to enable us to see these “far-away” numbers.

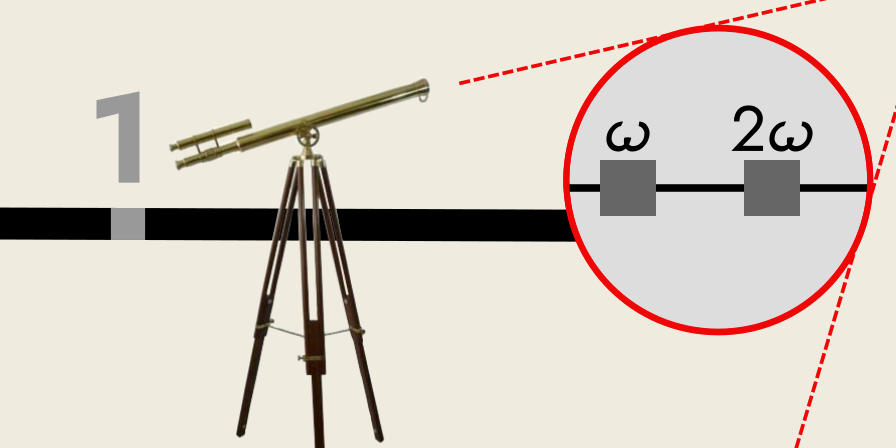
I’ve said enough about these hyper-reals for this article.

But I will be borrowing this notion of “zooming” for the indefinite numbers.

My issues with the infinite

While these hyper-reals, and the logical machinery that grounds them, are all very impressive, I have some reservations with the concept of infinite quantities (both large and small).

The idea that there is a quantity, 𝜔, that is larger than an endless sum (i.e. 1 + 1 + 1 + 1 +…) makes no sense to me.

It seems a fundamental fact of reality that given a small quantity and a larger quantity, continually adding to the (initially) smaller quantity will eventually cause it to be greater than the second (initially) larger quantity.

Yes, a million is larger than a thousand.

But, if we keep adding to the thousand, we will eventually exceed the million.

And likewise, for all possible pairs of quantities.

This is referred to as the Archimedean property.

It states that there are no infinitely small or infinitely large quantities.

It is attributed to Archimedes, but existed in Greek thought before he was even born (appearing in Book V of Euclid’s Elements).

Obviously, the Archimedean property does not apply to the hyper-reals.

You can keep adding finite quantities together, forever, and still not exceed the infinite hyper-real 𝜔.

Yes, I understand that mathematicians can design formal systems with arbitrary properties.

They can take this property and that property, working out the consequences of these decisions.

Fine.

But what I am interested in, my Alpha and Omega, is reality itself—and in making mathematics relevant and intelligible to people.

And for that reason, I will avoid using actually infinite quantities (and thus the hyper-reals).

But I will carry forth their spirit in my own solution, the indefinite numbers.

(I’d note that I am in good company in this regard, as Robinson himself once said: Infinite totalities do not exist and any purported reference to them is, literally, meaningless…)^[4]

Finite infinitesimal and unlimited numbers

Can we get the benefits of infinite numbers, without actually using the concept of infinity?

To eat our infinite cake, and still have it?

“Yes” I say.

And here’s how.

We use humongous numbers.

Numbers so big, there isn’t enough space in the universe to write them down.

Numbers so big, we don’t even know now big they actually are.

But these numbers are still finite, despite their humongous size.

Am I mad, or do such numbers actually exist?

Indeed they exist.

And we will discuss them shortly.

First though, I want to truly emphasize just how humongous these numbers are.

They are very, very big.

Incomprehensibly big.

To convey just how humongous they are, it helps to know a little about exponential notation.

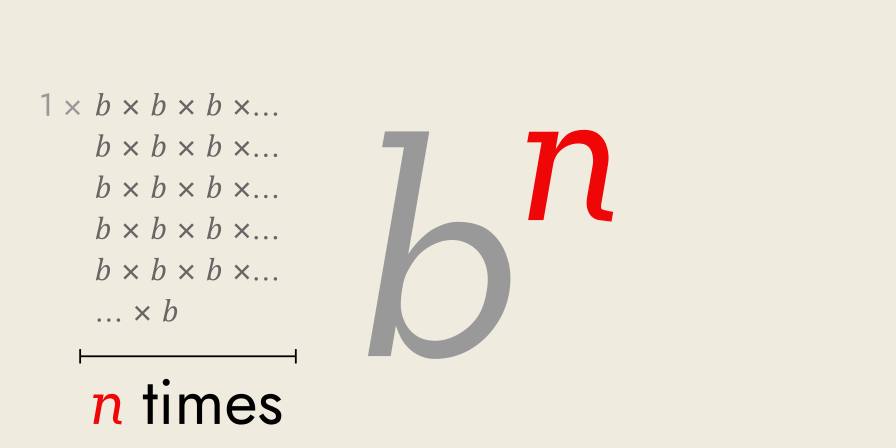
Exponential notation describes numbers in terms of repeated multiplication by themselves.

It is a useful shorthand for writing out large numbers.

An exponential number is a number of the form: 𝑏^𝑛
Where:

• 𝑏 is called the “base”
• 𝑛 is called the “exponent” (or power), meaning the number of times 𝑏 is multiplied by itself.

A simple example would be: 2⁴
= 2 × 2 × 2 × 2
= 16

There are different forms of exponential notation.

“Scientific notation” is an exponential notation of the form: 𝑏 × 10^𝑛
Where 𝑏 is a decimal number, with only one digit to the left of the decimal point. It is commonly used by scientists.

An example would be the number 1,324 that is re-written as: 1.324 × 10³

Exponential numbers grow fast:

• At 10⁰, we have one thing.
• At 10³, we have one thousand things.
• At 10⁶, we have one million things.
• At 10⁹, we have one billion things.

Remember this rapid growth as we now discuss these humongous numbers in more detail.

Google the googolplex and Graham’s number

In 1920, the mathematician Edward Kasner was walking with two of his nephews, Milton and Edwin.

Their uncle was trying to teach them the difference between incomprehensibly large numbers and infinity.

He wanted a word for a number that was written as “1” followed by one hundred zeroes: 10,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000,​000

Or 10¹⁰⁰ (for short).

Between them, they came up with “googol”.^[5]

And the name stuck.

It stuck so much that the two guys behind “Google”, the famous tech company, used it for their company name.

“Googol” got misspelled as “Google” in the process, but the term “googol” is the ultimate origin of the name “Google”.^[6]

How big is a googol?

There are about 10⁸² atoms in the universe, so it seems a googol is a very large number indeed.

In fact, a googol is one billion billion times larger than the number of atoms in the universe!

So, this is an incomprehensibly large number.

But, at least we can write it down—with a bit of effort in decimal format (a hundred zeros!), and very easily in exponential format (10¹⁰⁰)

Another number they named that day in 1920 was a “googolplex”, which is a “1” followed by a googol of zeroes.

That is: 10^googol

How big is a googolplex?

Well, it is so big, that it is impossible to write it out fully in decimal format, e.g. “10,000,000…”.

There isn’t enough space in the universe to write it out in decimal form, let alone comprehend the number of things it represents.

But, at least we know what a googolplex looks like.

It can be written, in full, using exponential notation as: 10^{10,​000,​000,​000,000,​000,​000,000,​000,​000,000,​000,​000,000,​000,​000,000,​000,​000,000,​000,​000,000,​000,​000,000,​000,​000,000,​000,​000,000,​000,​000}

This is clearly a humongous number.

(Remember, 10⁹ is a billion!)

Edward popularized both “googol” and “googolplex” in his 1940 book “Mathematics and the Imagination”.^[7]

Now, can we go even higher?

Can we create numbers that make a googolplex look small?

”Yes We Can!”, as the slogan goes.

Graham’s number is one such number: a number so vast and incomprehensible, we don’t even know how large it is.

It was used by Ronald Graham to explain the upper bounds of a problem he was working on in the 1970s,^[8] and we still only know the right-most digits (e.g. …95387 etc.) and not the number in its entirety.

We cannot write it in exponential format (e.g. 10¹⁰⁰ etc.), since there isn’t enough space in the universe, even using exponential notation.

In fact, specialized forms of notation had to be created just to deal with numbers this big.

And don’t forget: there are an infinite number of numbers that are even bigger than Graham’s number.

And yet—all of them are finite in size.

So, to my earlier point: we don’t need infinity to reach the incomprehensibly large (or small).

The indefinite numbers, both large and small

We’ve seen that numbers exist that are so large, we cannot fully quantify them.

I’ll call these numbers the unlimited indefinite numbers.

They are indefinitely large, yet finite.

Since these numbers are unlimited, I’ll represent them with the italic Greek uppercase letter upsilon, 𝛶.

“U” for unlimited,“u” for upsilon. Uppercase because it is big.

(Italic since it is a variable, which means it can stand for any unlimited indefinite number.)

If you take the number one, and divide it by an unlimited number, 𝛶, you’ll get an incomprehensibly small number.

This number will be so small, we cannot fully quantify it.

I’ll call this indefinitely small number an infinitesimal indefinite number.

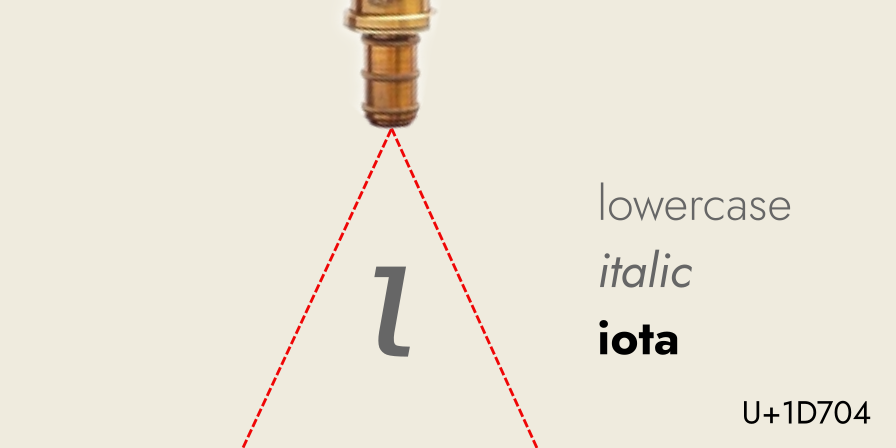
Since these numbers are infinitesimal, I’ll represent them with the italic Greek lowercase letter iota, 𝜄.

“I” for infinitesimal, “i” for iota. Lowercase because it is small.

(Italic since it is a variable, which means it can stand for any infinitesimally indefinite number.)

These infinitesimals are indefinitely small, yes, but not infinitely small.

Like their unlimited counterparts, they are still finite.

(The word “iota” means “an extremely small amount” in English—exactly what I intend with these infinitesimal numbers.)

Think of infinitesimal, 𝜄, and unlimited, 𝛶, indefinite numbers as a concept: some quantity that can be as small as you like, or as big as you like, without ever being expressible in ordinary notation.

At all stages of our mathematical development, we encounter problems we cannot solve with the mental tools available to us.

Negative numbers. Irrational numbers. Complex numbers.

All introduced to solve problems that could not be solved (or even described) using the existing concepts.

And so it is with the infinitesimal and the unlimited indefinite numbers.

This approach has a long history, wonderfully expressed in this quote from Leibniz:

It will be sufficient if, when we speak of infinitely great (or more strictly unlimited), or of infinitely small quantities (i.e., the very least of those within our knowledge), it is understood that we mean quantities that are indefinitely great or indefinitely small, i.e., as great as you please, or as small as you please, so that the error that any one may assign may be less than a certain assigned quantity.

…Thus, by infinitely great and infinitely small, we understand something indefinitely great, or something indefinitely small, so that each conducts itself as a sort of class, and not merely as the last thing of a class.

… it will be sufficient simply to make use of them as a tool that has advantages for the purpose of the calculation, just as the algebraists retain imaginary roots with great profit.

Simple sums with the indefinite numbers

I’ll finish with examples of arithmetic using the indefinite numbers, leading to practical applications later.

The indefinites might seem strange, but they behave like “normal” numbers in many regards.

We can add and subtract indefinite numbers (that are of the same scale), just like we can with regular numbers.

We can add infinitesimal indefinites together: 𝜄 + 𝜄 = 2𝜄

Same for the unlimited indefinites: 𝛶 + 𝛶 = 2𝛶

Break a length of one unit into a million (1,000,000) equal pieces, and each piece is a millionth (0.0000001) of a unit wide.

That is: 1 ÷ 1,000,000 = 0.0000001

So, a whole number that is large (a million), has an exact counterpart that is small (the millionth).

We call these pairs of numbers reciprocals.

As mentioned, reciprocals are multiplicative inverses: when one is multiplied by the another, you get the number one.

That is: 1,000,000 × 0.0000001 = 1

The indefinite numbers also come in reciprocal pairs: one large, the other small.

Break a meter stick into an unlimited number of pieces, 𝛶, then each piece will be infinitesimally small, with a width of 𝜄: 1 ÷ 𝛶 = 𝜄

So, if you have 𝛶 pieces, and each piece is 𝜄 wide, then you will have 1 unit: 𝛶 × 𝜄 = 1

The best human eyeballs can see down to 1/10^th of a millimeter, i.e. 1/10,000^th of a meter, i.e. 0.0001 m.

From our perspective, anything smaller than this cannot be detected.

So, two lengths that differ by less than 0.0001 m will look the same to us.

This notion of “equal, from one perspective, but different from another perspective” is very important.

It is different from the normal meaning of “equal” (=).

The normal use of “equality” means “has the same (numerical) value” or “gives the same (numerical) result”.

The sums:

• 2 + 3 = 5
• 3 + 2 = 5

Are equal in the normal sense, since both additions give the same end result, despite the different order of the summands (“2” and “3”).

When we work across scales, e.g. adding an infinitesimal to a regular number, it is not the usual notion of “equality” that applies.

I’ll introduce the symbol ≅ to mean “equal, from a given perspective, but different from another perspective”.

This is similar to Fermat’s concept of “adequality”, where he discarded traditional infinitesimal differences between finite quantities.

It doesn’t mean that two numbers are “almost equal”, which has the following symbol: ≈.

The number 99 is almost 100, but we can easily tell them apart from our regular perspective.

If we add an iota, 𝜄, to something, nothing seems to have changed (from our regular perspective): 1 + 𝜄 ≅ 1

Consider adding a carbon atom to the end of a meter stick.

A carbon atom is about 0.0000000002 m wide, so the meter stick is now longer, but our eyeballs cannot detect a difference.

That is: 1 m + 0.0000000002 m
= 1.0000000002 m
≅ 1 m

Just like when we added one iota, 𝜄, to one unit length, 1.

Yes, we increased the length of the meter stick.

But, an iota of a difference is too small to detect.

Thus, from our normal perspective, we still have a stick of one meter in length: 1 + 𝜄 ≅ 1

If we “zoom” in though, using a magic mathematical microscope, we can “see” the difference.

This principle of “the same from one perspective, but different from another perspective” is key to the use of indefinite numbers in a range of applications.

I could write a lot more on the arithmetic of these new numbers, but I’ve covered enough for now.

In my next article, I’ll put the indefinite numbers to good use, as we figure out the area of a circle (one of the key discoveries of Archimedes). ∎