Multiplying Bananas by Umbrellas

Multitudes by Multitudes

I took the title for this article from the amusing and insightful 1974 article (of the same name) by Professor Eric. R. Laithwaite.^[1]

He tackles the widespread confusion among professionals and students regarding the adding and multiplying of quantities of a different type.

Allegedly, we cannot add apples to oranges, but we can:

multiply mass by acceleration to get force.
multiply electrical resistance by current to get voltage.
multiply mass by the speed of light (squared!) to get energy.

And so on.

He is critical of academics who fail to explain this rather counter-intuitive action, and who merely insist that people accept the result, without explanation.

I read the article recently, and I recalled having read a discussion of this very matter in a book, many years ago.

The book is called “Mathematics is About the World”, by Dr. Robert E. Knapp, and it is the ultimate inspiration for the Reduct blog.^[2]

It was the first book I read that explicitly showed where mathematics “came from”—how it was derived from the real world, and intimately related to it.

I will be using Dr. Knapp’s discussion as the basis for my explanation of “products” of quantities, and show how Dr. Knapp’s approach provides an answer to the objections raised by Professor Laithwaite.

Comparing apples and oranges

adding an apple to an orange equals a '?' — What is the sum of an apple and an orange?

Can we compare apples and oranges?

There is a common phrase that suggests we cannot.

Saying “comparing apples and oranges” implies that no sensible comparison can be made, since they differ in a fundamental way.

However, via abstraction, we can compare apples and oranges.

We can compare them and place them into the same higher-level conceptual group of “fruit”.

In doing so, we ignore the concrete differences between them (color, shape, texture etc.), and focus solely on their common origin—as the mature and ripened ovaries of flowers.

Can we add apples to oranges?

Yes.

adding an apple to an orange gives two fruit as its sum — Defy everyday logic and add apples to oranges!

When we add two multitudes of different kinds, we get a third multitude, representing the sum of the first two multitudes.

(A “multitude” is a group of individual things: a group or a crowd etc.)

We just focus on the relationship between the numbers involved, and treat the units separately:

= 1 apple + 1 orange = 1 + 1 apple + orange

And what is the unit of this third multitude?

Obviously, it is a collection of things—but what are the things in question?

In this case, it is “fruit”, as an abstract category: = 1 + 1 apple + orange = 2 fruit

We add an apple to an orange and get two fruit.

Simple, eh?

Let’s go further.

Multiplication as arrangement-in-an-array

4 × 3 = 12 — A simple multiplication with its fancy monikers.

I’ve said it before—there are many interpretations of multiplication.

The one I will consider here is the “arrangement in an array” interpretation.

You have to multiply two numbers together: four and three, for example.

In mathematical jargon the numbers to be multiplied are usually called the “factors” of the multiplication.

The number to be multiplied (4) is the multiplicand, and the number by which it is multiplied (3) is called the multiplier.

Their order matters, as we shall see.

How is this multiplication by arrangement in an array done visually?

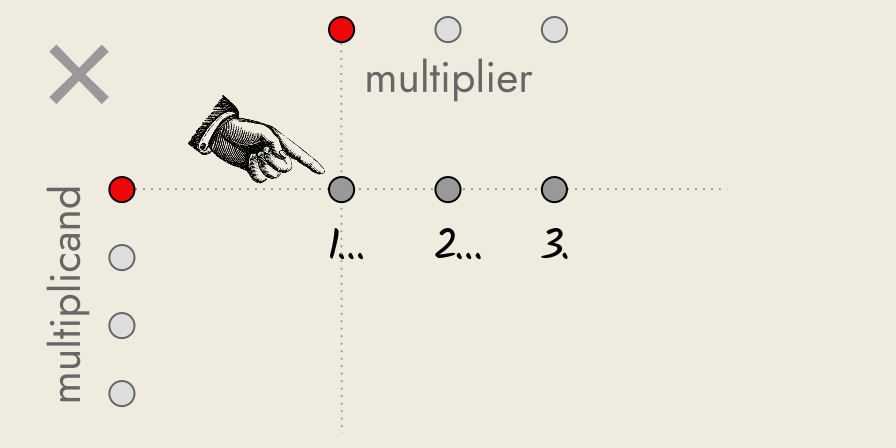
one row of 4 dots are multiplied by 3 dots — We start at the top and count left-to-right, row-by-row.

We start with the first number, 4 (the multiplicand), and for every unit making up this number, we add a group of three units (the multiplier) to a running total.

We iterate over all four units, adding to our running total at each step, and the result is a rectangular array of twelve units.

This array of twelve units is called the product of the multiplication and represents the end-point of the process.

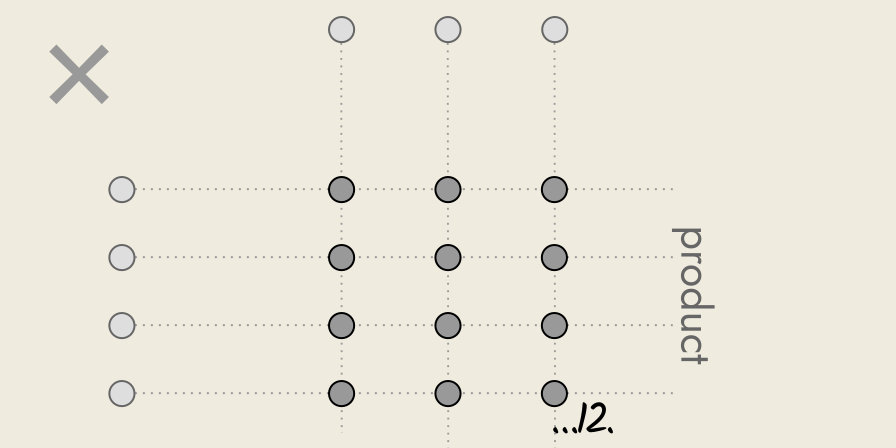
all rows of 4 dots are multiplied by 3 dots, to give a rectangular array of 12 dots. — We end with an array of 12 dots: 4 rows and 3 columns.

This is how all multiplication by array arrangement is done, regardless of the individual things we are multiplying:

First, we focus on the arithmetic of the numbers involved.
Then, we figure out the appropriate units, always referring to physical reality to guide us.

We will use this same process shortly to multiply bananas by umbrellas (as silly as that might sound).

Do things look different if we switch the order of the factors?

That is, multiply 3 by 4?

We repeat the same process of “arrangement in an array”, except this time we start with three units, and for every one of these three units, we add four units to our running total.

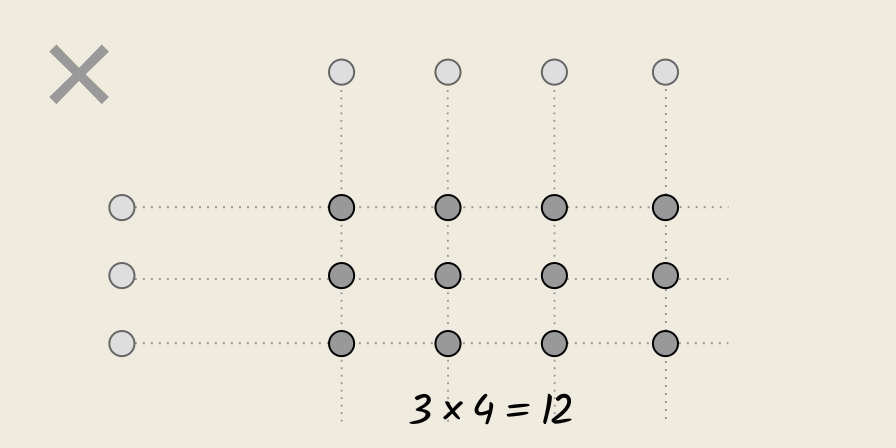
a 3 × 4 array is shorter but wider than a 4 × 3 array. — A 3 × 4 array is shorter and wider than the previous 4 × 3 array.

As before, we get an array of twelve units, but this time its dimensions are different.

Now, we have a 3 × 4 array: it is wider (but shorter) than the previous 4 × 3 array.

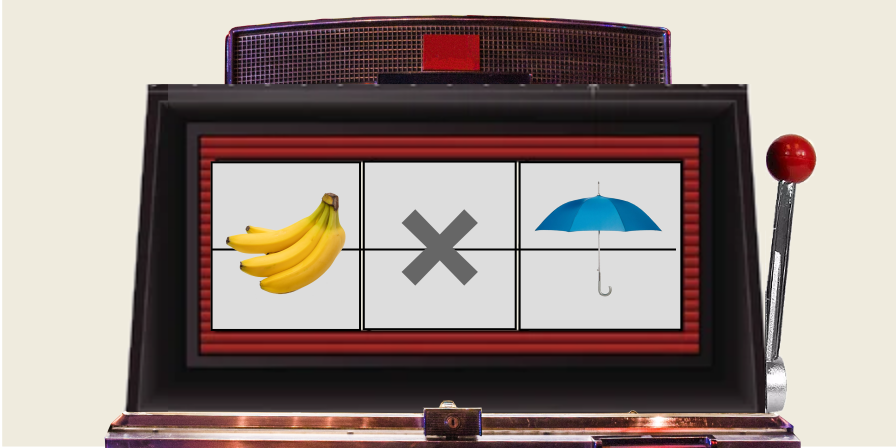
Multiplying bananas by umbrellas

When one multiplies a number of units of one kind by a number of units of a second kind, the result is a number of units of yet a third kind.

Robert E. Knapp. Mathematics is About the World, 1^st edition, 2014, p. 156. Kindle Edition.

Finally we come to the ridiculous sounding multiplication stated in the title of this article: the multiplication of bananas by umbrellas.

Given the obvious differences between bananas and umbrellas—how can they be compared?

Earlier, we saw that we can add apples and oranges by:

placing them both under the same category (“fruit”), and
following the normal scheme of adding multitudes together.

Similarly, we can place bananas and umbrellas under the very general abstract category of “thing”.

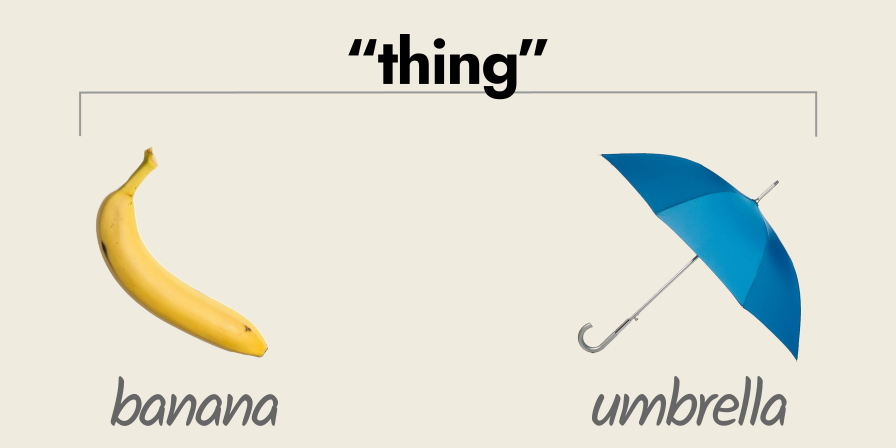
both a banana and an umbrella can be grouped under the category of 'thing'. — Both of these are “things”.

A banana is a “thing”, and an umbrella is a “thing”, i.e. an inanimate, physical object.

Using the scheme of multiplication as arrangement-in-an-array, we can now multiply a number of bananas by a number of umbrellas.

Consider multiplying three bananas by four umbrellas.

Again, for each of the three bananas, we add four “things” to our running total.

Since the units (“banana” and “umbrella”) are different, we abstract them into the higher level concept of “thing”, and we focus on the numbers (3 and 4) involved.

So, at each iteration, we add four “things” (as a general concept) to our running total of “things”.

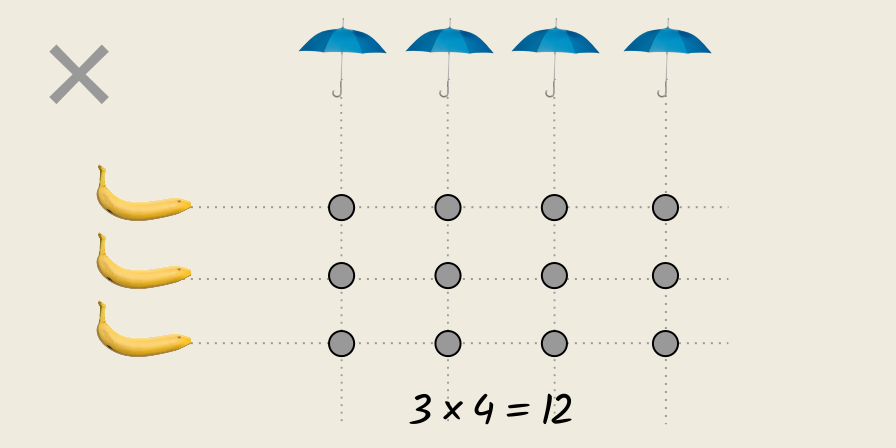
an array of 12 'things' created from 3 bananas multiplied by 4 umbrellas. — Mystery solved!
The multiplication of bananas by umbrellas.

This unit (“thing”) is like the earlier unit of “fruit”: it is more abstract than the units of the factors of the multiplication (bananas and umbrellas), and subsumes them.

We don’t create some mutant object, a banana-umbrella or umbrella-nana, or anything like that.

an umbrella with a banana for a handle, the 'umbrella-nana'. — The umbrella-nana.
(which is still a “thing”)

We just keep track of the number of things involved, and file each result under our new, broader category of “thing”, which is the unit of the product (the end-result).

After completing our multiplication, we now have 12 things.

So, the multiplication of bananas by umbrellas is not as ludicrous as it first seems.

We can make it sensible and consistent to multiply multitudes of a different type.

To recap the process for the combination of two multitudes of a different type:

First, we focus on the arithmetical relationship between the numbers involved.
Then, we figure out what the new unit should be (for the sum or product).

Let’s move from combining multitudes of different types, to combinations of multitudes and magnitudes.

Multitudes by Magnitudes

When we added apples to oranges (or multiplied bananas by umbrellas), we were combining multitudes of different types, where a multitude is a group of individual things.

Now, we come to combining multitudes with magnitudes, where a magnitude is a continuous physical property, e.g. time or length.

The mythical man-hour

the man-hour as the conceptual multiplication of man by hour

What is a man-hour?

It is not a rate like “men per hour” nor the “amount of work done per person per hour”.

Rather, the “man-hour” is a unit, used to compare the amount of “work” done by a person working constantly for an hour, against other tasks to be completed:

number of people × number of hours = man-hour

The man-hour is definitely related to the rate of “amount of work per person per hour”, as we will see.

The concept of “man-hour” can make it easier to calculate the resources required for a project—which is why it is widely used in project management to estimate the time and money required for various tasks.

So, the man-hour is a unit used to measure an amount of work.

What sort of work?

Well, it depends on the context.

For a construction company, it could be “blocks laid” or “ditches dug” or “boilers installed”: any relevant amount of work, basically.

Assume, on average, 50 blocks are laid per man per hour.

This is a multi-part rate, written as: 50 blocks / 1 man / 1 hour

Grouping the numbers to the left, and the units to the right, and doing our sums, we get:

50 ÷ 1 ÷ 1 blocks / man / hour

= 50 blocks / man / hour = 50 blocks / man-hour

How did we go from “blocks / man / hour” to “blocks / man-hour”?

Well, when you are doing repeated divisions, you can re-write it as a single division (just two terms) using the product of the divisors.

If you haven’t seen this technique before, it can be confusing, but I’ve given an example in the footnotes*.

So we have this new type of unit, a “man-hour”, which is a number of people (a multitude) multiplied by a unit of time (a magnitude).

Seems a bit of a strange sort of thing, doesn’t it, this man-hour?

A compound unit of multitude (man) and magnitude (time), taken together as a single entity.

Can we visualize it and make sense of it, as a concept?

I believe so.

Making sense of man-hours

a stick figure of a man, combined with an hour glass, as a 'man-hour', with question marks behind him

When making sense of the man-hour as a concept, perhaps the best place to start is to state what it is not.

The man-hour is not a rate like “men per hour”.

If, on a certain day, 72 men cross a given bridge, then we can write the following rate: 72 men / 24 hour = 72 ÷ 24men / hour = 3 men / hour

But the man-hour is not a rate like “men per hour”.

It is a unit.

And rather than being a simple unit, like length or time or area, it is a combination of two different things: a multitude (man) and a magnitude (time).

It is a compound unit.

Trying to visualize the man-hour might seem impossible, but I see it as a conceptual fusion of man and hour.

We could see it like a stick figure merged with an hourglass, or a man in a clockface—whatever works!

The important thing in any visualization, is that it conveys the compound nature of the man-hour: it is not one thing or another, but both together.

And like any unit, the man-hour is used to “count off” against things in the world—that is, it is used to measure things.

And what things is the man-hour used to measure?

The time taken to complete tasks.

(And since “time is money”, the man-hour can also be used to measure the cost of tasks.)

Putting man-hours to work

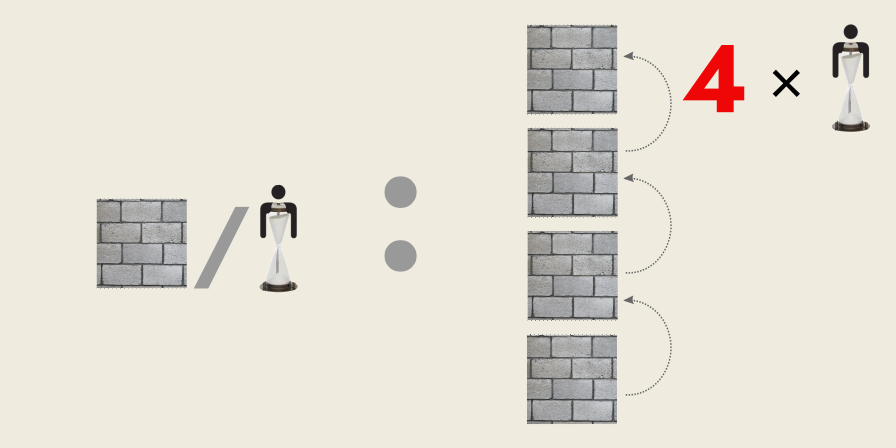
measuring the rate of 50 blocks per man-hour, against the workload of 200 blocks — Comparing a workrate of 50 blocks per man-hour, against a task requiring 200 blocks to be laid.

The man-hour is used as a unit for estimating the time and/or money required for a given project.

Example: a construction site foreman knows that 50 blocks can be laid by the average block-layer per hour.

That is, the average work rate is 50 blocks per man-hour.

The foreman has been asked to estimate the time to build a wall requiring 200 blocks.

How would he do this?

Easy.

If 50 blocks take one man-hour, then we can compare this rate of work to the amount of work to be done, of 200 blocks.

50 blocks / 1 man-hour : 200 blocks / ? man-hour

By counting off the 50 blocks against the 200 blocks, we find the 200 blocks are four times greater than the 50 blocks, in quantity: 200 blocks / 50 blocks = 200 ÷ 50 blocks / blocks = 4 ~~blocks~~ / ~~blocks~~ = 4

Thus, we need four times more man-hours.

Now the foreman knows that four man-hours are needed for the wall.

The foreman can either have one block player work on it for four hours: 1 man × 4 hours = 4 man-hours

Or the foreman can have four block layers work on it for one hour: 4 men × 1 hour = 4 man-hours

The end result is the same either way: 4 man-hours.

The mythical woman-month

four icons of pregnant woman, lined up in a row

Having written about “man-hours” it seems only fair that I now consider the fairer sex.

Let’s invent a new unit: the “woman-month”.

A woman-month is used to measure the amount of work done by one woman, in one month’s worth of work.

And what will we measure with this newly minted unit?

The peculiarly female state of pregnancy seems fitting.

Typically, it takes one woman a total of nine months to complete one pregnancy.

We can write this as a multi-part rate: one pregnancy per one woman per nine months

Or, in slightly more mathematical notation: 1 pregnancy / 1 woman / 9 month = 1 ÷ 1 ÷ 9 pregnancy / woman / month = ¹⁄₉ pregnancy / woman-month

Thus ¹⁄₉ of a pregnancy is completed in one woman-month, and so nine woman-months are needed to “finish the job”, so to speak.

Now, what if we wanted to make the pregnancy finish faster?

What if we wanted the pregnancy done in one month, rather than nine months?

Like the man-hour, the woman-month can be increased by either:

increasing the number of women, or
increasing the number of months

That is: 1 woman × 9 months = 9 woman-months

And: 9 women × 1 month = 9 woman-months

Could we just add in more women to get the pregnancy completed faster?

Let’s do some sums.

If we had nine women, that would be nine woman-months of “capacity”, wouldn’t it?

And we could just multiply our rate of pregnancies per woman-month by nine, since now have nine times more women: 9 × (¹⁄₉ pregnancy / woman-month)

Giving us: 1 pregnancy / 9 woman-month

But, this time, we have completed the pregnancy in only one month (since we have nine women).

Makes sense, yes?

No!

Of course not.

It is complete nonsense to suggest that nine women can complete a pregnancy in one month.

That is not how the process works, as we all know.

It takes an individual woman nine months (on average) to complete one pregnancy, and that is it.

There is no further arithmetic that can be done.

Why did I even bother with this ludicrous example?

Because I wanted to emphasize the danger (and absurdity) of swapping our judgement for arithmetic.

Sure, we can invent concepts and units like the man-hour and the woman-month (and others still!)—but if they do not match the reality of the situation, then they are worse than useless (since they can lead us astray).

There is a famous book in the field of software development, “The Mythical Man-Month” by Fred Brooks.^[3]

The book’s central theme is this: adding more people to a project, which is behind schedule, makes it take longer.

The use of man-hours, or man-months etc., implies a simple arithmetic: the more people you have, the shorter the time it will take them to finish the work.

This sort of simplistic analysis may be fine for straight-forward tasks like digging a ditch etc.

In other fields (like software development), adding more people complicates matters, which may delay a project further: more lines of communication, more in-fighting, more onboarding etc.

And, as we have seen, assuming simple arithmetic in real-world systems can lead to absurd conclusions: like nine women making a pregnancy happen in one month.

Magnitudes by Magnitudes

Finally, we come to the multiplication of magnitudes by magnitudes.

And by “magnitude”, I mean a continuous physical quantity like time, weight or distance.

Multiplying magnitudes includes some of the most important concepts in science, from the everyday to the utterly abstract:

Momentum, p, the amount of motion or “push” in an object, given by mass, m, and velocity, v : p = m × v
Voltage, V, the amount of electrical force (or “push”) in a circuit, given by current, I, and resistance, R: V = I × R
Energy, E, a concept so abstract I can’t even begin to explain it, given by mass, m and speed of light (squared), c ²: E = m × c ²

I won’t be covering E = m × c ², but I will discuss momentum, along with another product quantity that you’ve probably never heard of: the kilogram-metre.

Kilogram-metre

The kilogram-metre (kg·m) is a combination of:

an amount of stuff, i.e. “mass” (measured in kilograms), and
a distance (in metres).

For clarity, I use the interpunct “·” to separate the “kg” and “m” symbols.

The kilogram-metre can be used as a unit to compare the moving of different amounts of things over different distances.

How is the kilogram-metre (a unit) different from a kilogram per metre (a rate)?

Very!

Just look at the following image:

kilogram spread over a metre, equally, from left (0 kg) to right (1kg). — A rate of one kilogram per metre. Here, the kilogram and the metre are associated with one another, not fused together like the kilogram-metre unit.

The kilogram-kilometre (kg·km) is widely used in the freight and transportation industries, to measure various quantities. The kilogram-kilometre is one thousand times larger than the kilogram-metre: 1 kg·km = 1,000 kg·m

The kilogram-kilometre is a more convenient measure in these practical fields, since most journeys take several kilometres.

But the principle remains the same: both units are combinations of mass and distance.

What is the point of these units?

They are used to calculate various important business metrics.

Carbon dioxide (CO₂) emissions are very fashionable right now, with various schemes afoot to lower them to near nothing.

Different modes of transport emit different amounts of CO₂ per mass-distance of freight, as shown in the following table:^[4]

Mode	Type/Details	CO₂ (kg) per 1,000 kg·km
Van	< 1,300 kg; Petrol	1.089
HGV	> 17,000 kg; Rigid; 50% load	0.239
Rail	Freight train	0.025
Ship	Bulk carrier; 200,000+ dwt	0.003
Air	International; to/from UK	1.128

HGV: Heavy Goods Vehicle
dwt: Dead-weight tonnage. A measure of a ship’s cargo capacity, in metric tonnes (1 metric tonne = 1,000 kg).
UK: United Kingdom.
Figures for CO₂ (kg) rounded to three decimal places.
Table uses the “tonne-kilometre” as a unit, which is 1,000 kg·km (or 1,000,000 kg·m).

You want to calculate the CO₂ emissions of a journey.

How do you do it?

You take the total mass of the shipment (in kilograms, kg) and the distance travelled (in kilometres, km), say a 200 kg shipment over a 75 km distance.

Multiply the two together to get the total number of kilogram-kilometres (km·kg): 200 kg × 75 km = 200 × 75 kg·km = 15,000 kg·km

For your mode of transport you determine how many kilograms (kg) of CO₂ were produced per kilogram-kilometer.

If you used a van, then 1.089 kg of CO₂ were produced per 1,000 kg·km.

Then, calculate the total amount of CO₂ (kg) produced for the total number of kilogram-kilometres using the following formula: Total kilogram-kilometres × CO₂ per kilogram-kilometre

Putting in our numbers, we get: 15,000 kg·km × (1.089 kg / 1,000 kg·km) = 15,000 kg·km × (1.089 ÷ 1,000 kg / kg·km) = 15,000 kg·km × (0.001089 kg / kg·km) = 15,000 kg·km × (0.001089 1/km) = 15,000 × 0.001089 kg·km × 1/km = 16.335 kg·km/km = 16.335 kg

Then, 16.335 kg CO₂ (15 × 1.089 kg) is produced by our van, when hauling 15,000 kg·km.

Momentum

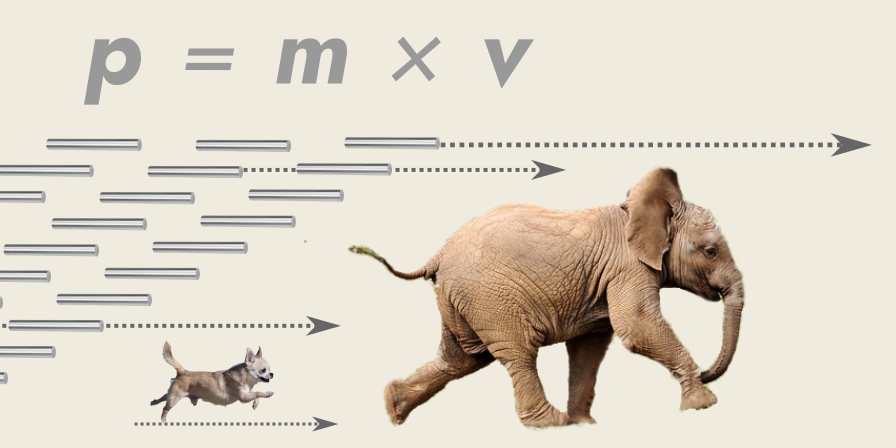
When a thing starts to move, it has something called momentum—a type of magnitude, which represents the “amount of motion” in the thing.

This “amount of motion” is affected by two properties of the thing:

the mass of the thing, which is the amount of stuff within it, measured in kilograms (kg), and
how fast it is moving in a particular direction, called its velocity, measured in metres per second (m/ s).

Momentum is a combination of two magnitudes—mass and velocity—and is calculated by multiplying them together.

That is, momentum is a product quantity, the result of multiplying magnitudes by magnitudes.

Momentum has the symbol p, from the Latin pellere (to push, propel or drive).

Why this concept of velocity rather than just speed?

Because direction matters.

Something running at you is very different to something running away from you, so we need to take account of the difference.

If we take West as our reference direction, then a man running West with a speed of 5 m/ s, has a velocity of 5 m/ s.

A woman running in the opposite direction (East) with the same speed has the opposite velocity of −5 m/ s.

I won’t go into further detail on this point, but it is an important aspect of momentum: it has a direction associated with it.

Anyways, let’s look at the practical aspects of momentum, using a Chihuahua and a baby elephant as examples.

If Chico the Chihuahua runs at you excitedly—no problem!

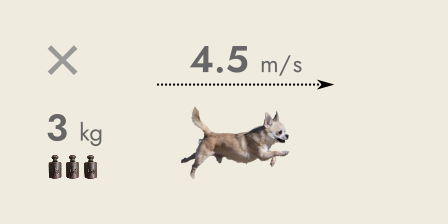
Chico the Chihuahua running. — All three kilos of Chico.

Chico doesn’t have much momentum, since an average male Chihuahua is about three kilograms and runs at about 10 miles per hour: p = 3 kg x 4.5 m/ s p = 3 x 4.5 kg·m/ s p = 13.5 kg·m/ s

However, if Dumbo the baby elephant runs at you—well then, you had better brace yourself!

Dumbo the baby elephant running. — All one hundred kilos of Dumbo.

His momentum is very much larger than Chico’s, thirty-three times larger, assuming the same velocity: p = 100 kg x 4.5 m/ s p = 100 x 4.5 kg·m/ s p = 450 kg·m/ s

If Dumbo hits you, he is probably going to hurt you—even if he was just trying to say “hello”!

At the very least, Dumbo is going to move you (unless you are massive yourself).

When writing about kilogram-metres (kg·m), I realized this unit gave another way to view momentum: as kilogram-metres per second.

This was new to me, and I haven’t seen it discussed elsewhere.

The typical approach is to treat momentum as the product of mass by velocity.

Whereas I can see it as the rate of kilogram-metres per second.

That is, as an amount of stuff moved per second.

What is the advantage of this alternative approach?

Well, a “moving bunch of stuff” is a pretty easy concept to grasp, and it has the advantage of harmonizing the concept of momentum with its mathematical calculation.

The typical approach of multiplying mass by velocity, makes less sense to me—it seems an abstract conception divorced from everyday life.

A way to calculate momentum rather than understanding it.

What does mass look like when multiplied by velocity?

Kilograms multiplied by metres-per-second?

What would that even look like?

mass (kg) × velocity (m/s) = ? — A product of magnitudes beyond my mind’s eye.

Personally, this is impossible to imagine, being far too abstract.

It is not like multiplying bananas by umbrellas to get a product of “things”, where a “thing” is a simple conceptual unit that I can imagine as a dot or generic counter.

The product of mass by velocity is measured in kg·m/s, and I cannot imagine what that looks like.

But an amount of stuff being moved per second, that I can visualize.

In our examples above:

Chico has a momentum of 13.5 kilogram-metres per second.
Dumbo has a momentum of 450 kilogram-metres per second.

If either of them run into you, you are going to experience a force equal to their momentum.

For Chico, this would be the force of 13.5 kilograms moving one metre in one second, i.e. p = 13.5 (kg·m)/ s

Chico’s momentum as 13.5 kilogram-metres per second — Chico’s momentum as a rate of kilogram-metres per second.

For Dumbo, this would be the force of 450 kilograms moving one metre in one second, i.e. p = 450 (kg·m)/ s

Personally, seeing momentum in this way (as a rate) is more natural than the typical view of momentum as a product of magnitudes. ∎

Footnotes

Why does dividing blocks by a number of men: blocks / man then by number of hours: blocks / man / hour result in the product quantity of man-hours? = blocks / (man × hour) = blocks / man-hour

The easiest way to explain repeated division is using repeated subtraction.

Consider the following difference: 100 − 2 − 10

We subtract 2 from 100, then subtract 10 from the result: 100 − 2 − 10 = 98 − 10 = 88

But, we could also start with 10, rather than 2: 100 − 10 − 2 = 90 − 2 = 88

“Same difference” as they say.

And rather than do two subtractions, one after another, we could just do one subtraction, by taking away the sum of the subtrahends: 100 − 2 − 10 100 − (2 + 10) = 100 − 12 = 88

And so it is with repeated division: we can just “bundle” up our divisions into one step, rather than go through repeated divisions.

An example will help, and I’ll use the division slash, /, rather than the division sign, ÷, to follow from the “50 blocks / man-hour” example above.

Consider the repeated division: 100 / 2 / 10

We have three terms, and by convention, we start dividing from the left: (100 / 2) / 10 = 50 / 10 = 5

Again, given: 100 / 2 / 10 Let’s start dividing with 10 this time, rather than 2: 100 / 2 / 10 = (100 / 10) / 2 = 10 / 2 = 5

The repeated division of 100 (by 2, and then by 10), can be turned into a single division of 100 by dividing by the product of the divisors (2 × 10): 100 / 2 / 10 = 100 / (2 × 10) = 100 / 20 = 5

So, as we can see, the answer is the same (“5”), regardless of the way we process the repeated division.

And, as it is for numbers, so it is for units—a repeated division of terms, can be expressed as a single division by the product of the terms: blocks / man / hour = blocks / (man × hour) = blocks / man-hour

[Back to text]

Key Takeaways

There is a sensible way to combine multitudes and magnitudes (of different types): first, focus on the arithmetic of the numbers involved; second, figure out the new unit (using reality as your guide).
Adding apples to oranges gives a sum of “fruit”, and multiplying bananas by umbrellas gives a product of “things”.
Combining multitudes with magnitudes, gives us product quantities like the man-hour and the woman-month.
Combining magnitudes together, gives us product quantities like the kilogram-metre and momentum.
Momentum can be viewed as a rate of kilogram-metres per second, rather than the typical product of mass by velocity.

References

Laithwaite, E. R. 1974. The multiplication of bananas by umbrellas. Electrical Review, pp. 822–824. Available at: http://www.gyroscopes.org/papers/The multiplication of bananas by umbrellas.pdf. (Accessed: 31^st October 2023). [Back]
Knapp, Robert E. 2014. Mathematics is About the World: How Ayn Rand’s Theory of Concepts Unlocks the False Alternatives Between Plato’s Mathematical Universe and Hilbert’s Game of Symbols. Kindle Edition. Self-published using CreateSpace Independent Publishing Platform. [Back]
Brooks, Frederick P., Jr. 1975. The Mythical Man-Month: Essays on Software Engineering. First Edition. Reading, Massachusetts: Addison-Wesley. Available at: https://web.eecs.umich.edu/~weimerw/2018-481/readings/mythical-man-month.pdf. (Accessed: 5^th November 2023). [Back]
Department for Energy Security and Net Zero and Department for Business, Energy & Industrial Strategy. 2020. Greenhouse gas reporting: conversion factors 2020. Available at: https://www.gov.uk/government/publications/greenhouse-gas-reporting-conversion-factors-2020. (Accessed: 6^th November 2023). [Back]