Science, Mathematics and the Modeling Relation

Mathematics’ mysterious effectiveness

The enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and that there is no rational explanation for it…

The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve.

How is that mathematical equations can predict things in the real world? That imaginary symbols, developed in isolation by mathematicians, can be used by scientists to describe the real world with astounding accuracy?

I’ve long been fascinated by this predictive power, especially in the case of mathematics. How is it that these squiggles on a page end up describing and predicting the behavior of things that didn’t even exist when the squiggles in question were first squiggled?

What sorcery is this!? What is at the root of this mysterious and miraculous effectiveness?

Is it just some sheer stroke of dumb luck? Or a sneak peek at a divine plan, a glimpse of an eternal and objective order?

What makes mathematics so effective?

It is difficult to avoid the impression that a miracle confronts us here, quite comparable in its striking nature to the miracle that the human mind can string a thousand arguments together without getting itself into contradictions, or to the two miracles of the existence of laws of nature and of the human mind’s capacity to divine them.

I’m not the only one be fascinated by this phenomenon. The physicist Eugene Wigner wrote an influential essay in 1960, “The Unreasonable Effectiveness of Mathematics in the Natural Sciences”,^[1] where he basically asks: “How can these squiggles on a page (mathematical symbols) predict things in the real world with such astonishing accuracy?”.

Wigner discusses the Newtonian theory of universal gravitation, but there are several examples. A personal favorite: “imaginary numbers” (square roots of negative numbers), which were invented as the solution to cubic equations in 16th century Italy. These “imaginary” numbers are now used to describe the behavior of electrical circuits and quantum mechanical systems, things totally unknown to anyone in 16th century Italy.

While Wigner concluded his essay with the notion that this was all a “miracle”, one that was a “gift which we neither understand nor deserve”, I intend to take a more grounded approach, one that leads to an actual explanation of the mysterious predictive power of science and mathematics.

Miracle, mystery or dumb luck?

Is knowledge of mathematics really knowledge of the timeless and eternal, a sneak peek at a divine plan? Or is it just dumb luck that these experiments and squiggles can be so consistently useful?

To me, it seems unlikely to be just dumb luck—the effect is too consistent across too many fields to be pure chance.

A miracle then? Certainly, it might seem to be the case at first glance—and many have adopted this view! But do we need to resort to mysticism and the supernatural to explain the real-world impact of science and mathematics?

“No” is my answer, and I’ll explain the “unreasonable effectiveness of mathematics” (and science in general) in terms of a little‐known concept known as the “modeling relation”,^[2] a concept I first encountered in the work of Robert Rosen—one which deserves a much wider audience.

Science, mathematics and the modern world

A scientist may be thought of as having access to a great store of patterns into which he delves to find one that will fit the facts he seeks to integrate into a theory…

Success may come later in this field because some mathematician, possibly quite ignorant of his concern, has worked out a pattern which will now suit the phenomena.

Our modern world has been made possible by science and mathematics. Everything from skyscrapers to space rockets, ocean liners to the internet, demonstrate the power of these subjects to predict and control our external reality.

Without them, we’d still be living in caves, chucking rocks at each other—rather than living in condominiums and firing cruise missiles at one another. (Plus ça change…)

But what are science and mathematics exactly? What is the relationship between them? And how do they give us such powerful and practical results?

Admittedly, trying to define science and mathematics is a bit like trying to define “democracy”: they mean different things to different people, and the singular labels of “science” or “mathematics” can rightly apply to many different actions and objects in the real world.

But, since “the beginning of wisdom is the definition of terms”, a working definition of both these concepts is essential. After defining them both, I will relate them together using Robert Rosen’s concept of the modeling relation,^[2] which will explain how the combination of science and mathematics has proved so powerful.

What is science?

Science is the systematic study of natural systems, where a “natural system” is some aspect of the real world that has been isolated for investigation. Examples of natural systems include a rock, a tree, a cloud etc., but also cities and solar systems.

To avoid being overwhelmed, we subjectively isolate aspects of external reality into manageable chunks: the physicist studies particles, the chemist chemicals, the microbiologist microbes, etc. But in truth, such divisions exist only in our minds, since “the whole universe is in a glass of wine.”^[3]

Scientists learn about the world through systematic investigations called experiments, where they either observe or interact with a natural system. Frequently, their experiments are guided by equations developed by mathematicians or “theoretical” scientists—with the “experimental” scientists seeking to confirm or refute the abstract predictions of their “theoretical” colleagues.

This deep link between mathematics and science has always fascinated me: it seems a profound mystery that the real world could be predicted with equations developed in isolation. But we will soon reduct this seemingly mysterious relationship, and understand its origin intuitively.

What is mathematics?

Now, if “science” is the systematic study of “natural” systems, what then is mathematics? I’ll borrow my favorite definition: “the study of mental objects with reproducible properties is called mathematics.”^[4]

What does this mean? Basically, the abstract objects studied (and invented!) by mathematicians have consistent properties. Numbers, geometric shapes, sets etc., exist only in the mind, but they have objective properties.

No, mathematical objects are not “physical” things, since they exist only in the mind; but neither are they purely subjective, like opinions, since they have objective properties, e.g. the area of a square, 𝐴, is the side length, 𝑙, multiplied by itself. Always.

These abstract systems of symbols, and their associated rules, are called formal systems. Where the scientist studies natural systems, the mathematician studies formal systems, learning about them via an iterative process of proof and refutation.

Formal systems are created by fiat (i.e. made up!) by their creator, who has full control of the symbols and rules of the formal system. Notably, we can still make surprising discoveries about formal systems: things not immediately obvious, like the Pythagorean theorem.

Causality and natural systems

There is a consistency to things in the real world: water is wet; things fall down, not up; the sun rises in the East and sets in the West, always.

Furthermore, events don’t just “happen” spontaneously, out-of-nowhere, without prior cause; even if we cannot determine the cause, it is there somewhere. Events lead from one to another according to fixed rules, and this orderly flow from one event to the next is called causality.

Causality makes the world knowable to the human mind, making the real world something we can understand and control (to a certain extent).

This is all very obvious of course, but it is important to point out that there are “rules” in the real world, and that we can conceptualize these rules as intuitive notions, e.g. “things fall down”.

When we make these intuitive notions rigorous and precise, we create “formal” systems, which we will discuss next.

Inference and formal systems

A formal system is a collection of symbols and precise rules for combining these symbols. The symbols might refer to something in the real world, or they might not: it doesn’t matter.

Think of arithmetic, where the symbols are the familiar numerals (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) and the operators on those numerals (+, −, ×, ÷).

We combine these symbols and operators together in precise ways, according to the rules laid down by the creator of the formal system, and we generate new statements in the language of the formal system, e.g. “1 + 1”.

The abstract things that make up the formal system are not “real” things, but their properties are fixed and reproducible. So, while they are “things of the mind”, they have objective properties.

Statements in a formal system, e.g. “1 + 1”, imply definite conclusions; in this case “1 + 1” implies “2”. We move from statement to statement according to definite rules, and we will call this process inference.

Inference in formal systems is the analogue of “causality” in natural systems, and we will now explore this connection in more detail.

The modeling relation, itself

On one hand, we have natural systems, the subject matter of science, bound by the rules of causality.

On the other hand, we have formal systems, the subject matter of mathematics, bound by rules of inference.

How can such different systems, natural and formal, be compared?

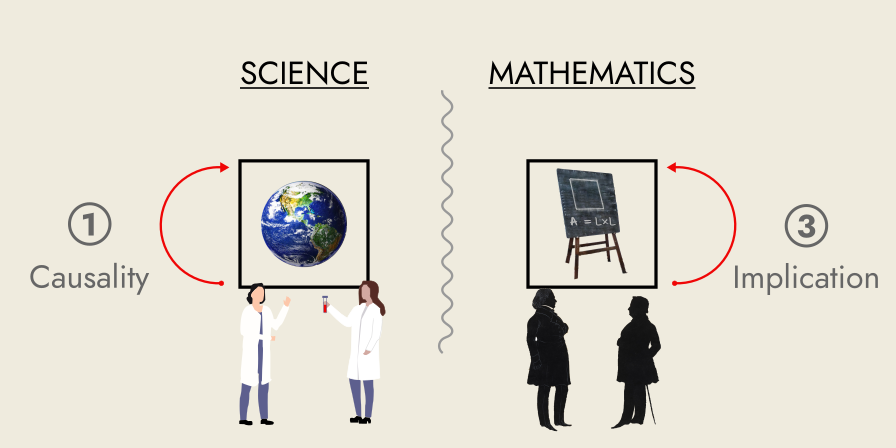
Well, causality and inference are two modes of entailment, fixed rules for how one thing leads to the next: an action to its subsequent effect, a statement to its inevitable conclusion.

Seeing that entailment exists in both natural and formal systems, we can bring the rules of causal entailment (in natural systems) into congruence with the rules of inferential entailment (in formal systems).

That is, we match the patterns of causal entailment in the natural system with the patterns of inferential entailment in the formal system.

Why bother?

Because matching these abstract patterns of entailment allow us to model the natural system using the formal system. By modeling, we can understand and predict the natural system, by studying the formal system.

Literally, we can replace the natural system with the formal one, and still maintain the entailment structure of the natural system under study.

Encoding and decoding

Now, having introduced the concept of modeling, our two systems (natural and formal) are still isolated from one another. To compare them, to complete the modeling relation, we need further two processes:

• encoding: how we get our natural system “into” the formal system, so we can begin the modeling process, and
• decoding: how we interpret the results of our model, so we can make predictions about the natural system.

• ---

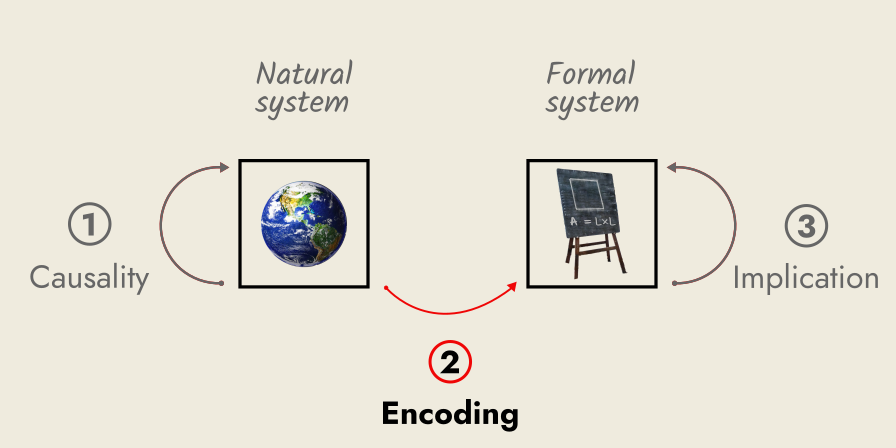
Encoding is the process of translating aspects of a natural system into the statements of a formal system. Typically, this is done through measurement, where we associate aspects of a natural system with a number in the formal system. Thus, encoding is an act of abstraction, where we focus on one part of a natural system, while ignoring the rest.

Decoding is the reverse process to encoding, where we go from the statements of a formal system back to aspects of a natural system. That is, we interpret statements in a formal system into claims about the natural system. Thus, decoding is an act of reduction, the tracing back of an abstraction to the real world.

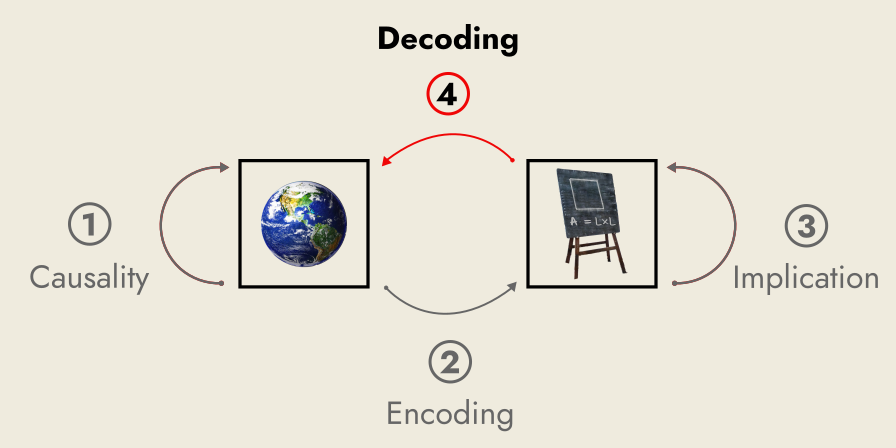
It is essential to note that the processes of encoding and decoding are not only independent of one another, they are also independent of the natural and formal systems they are used to translate between.

The everyday work of engineers, scientists and mathematicians involves the art of deciding what encoding and decoding procedures are to be used to establish modeling relations between different systems.

That is, how we should measure things in the real world (encoding), and how we should interpret the meaning of formal statements (decoding), are often subject to debate and discussion.

A shepherd counts sheep

To keep this discussion grounded, I will show the modeling relation “in action”, using the simple example of a shepherd counting his flock, as he buys and sells sheep over time.

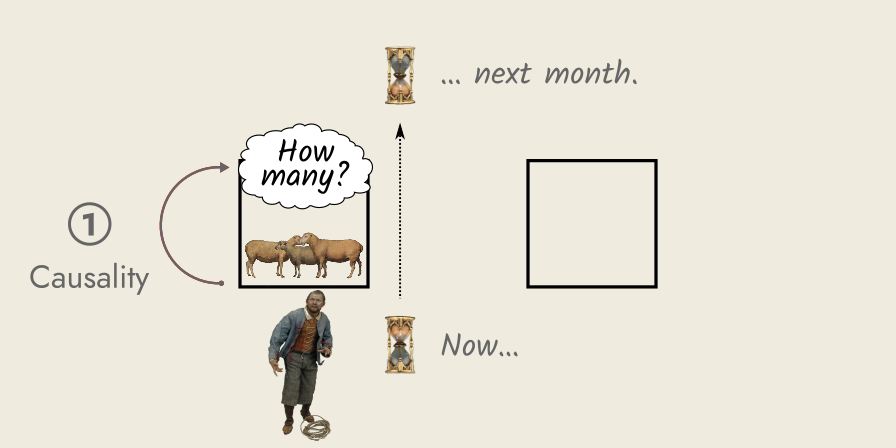
Our shepherd wants to know the size of his flock, so he can plan a round of buying and selling. In this case, our natural system is his flock of sheep, and our formal system is arithmetic, the familiar branch of mathematics.

To start the modeling process, the shepherd needs to encode his flock into the formal system of arithmetic somehow. In this case, encoding is simple: he counts his sheep.

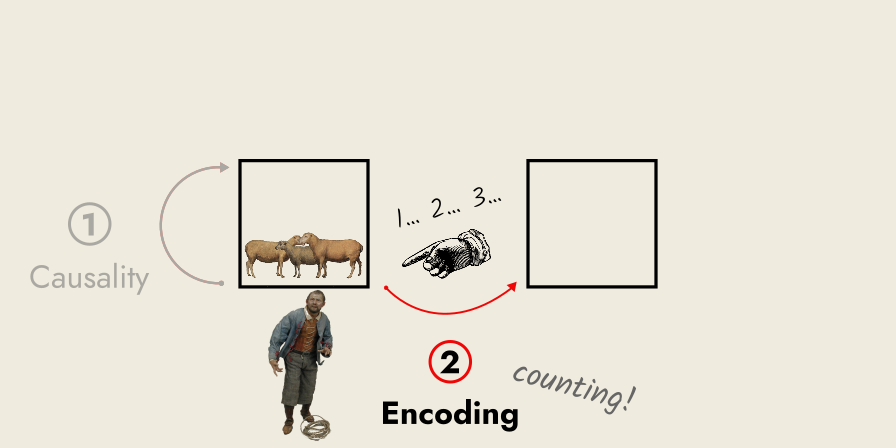
Counting is a measurement, an act of abstraction where we replace all the complexity of real things with a single number, a total.

After counting, he learns he has ten sheep. He can now replace all his woolly, four-legged things with the symbol “10” in the formal system of arithmetic.

Now, say he plans to buy twenty sheep and sell three sheep over the coming month. He thus creates a new arithmetical statement: “10 + 20 – 3”. The shepherd does his sums according to the fixed rules of arithmetic and generates a result, an arithmetical conclusion: “27”.

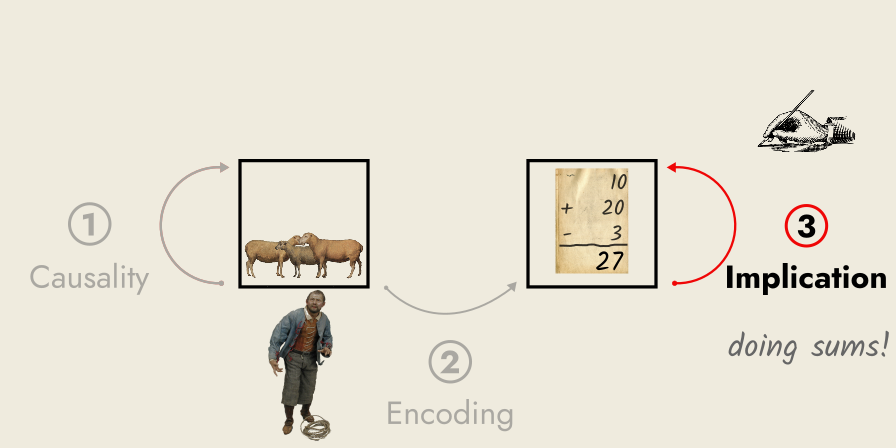
Being familiar with arithmetic and its relationship to the real world, the shepherd knows how to interpret this symbol “27”. Namely, he can decode this symbol into a prediction about the size of his flock, after all this planned buying and selling has completed.

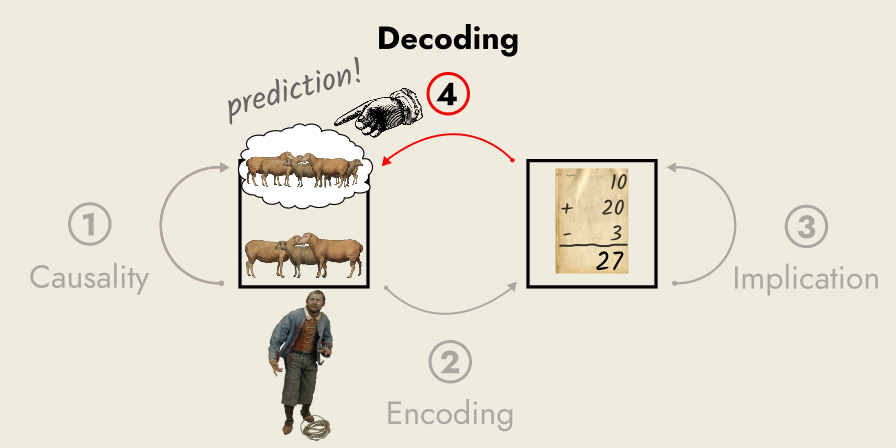
By modeling (doing his sums!), the shepherd doesn’t have to wait until all his transactions are complete to know the size of his flock: he can peer into the (possible) future through the formal system, and know the result in advance.

Modeling has many modes

In our simple example of counting sheep, we may not realize it, but what we are doing is modeling, something very profound, the foundation of how we understand and act in the world.

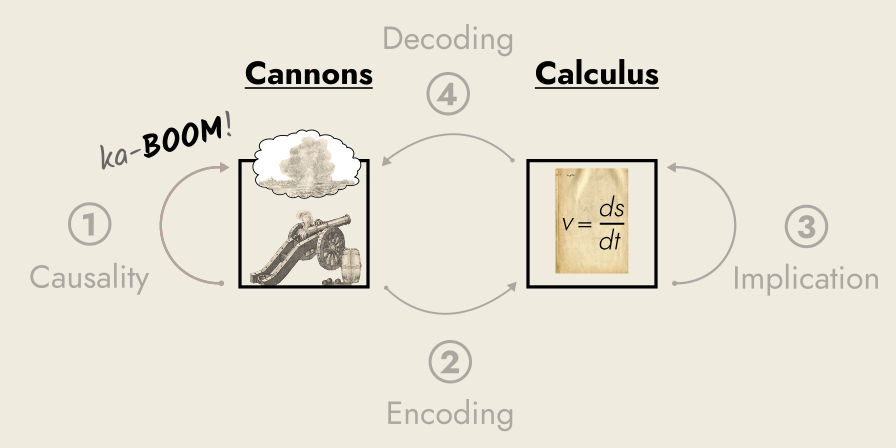
Every single example of modeling natural systems with formal ones, follows the same pattern as we saw with the shepherd: bringing into congruence the entailment structures of the different systems. Whether using complex numbers to model electrical circuits, or using calculus to predict the path of cannonballs, the principle is the same.

Furthermore, we are not confined to modeling natural systems with formal ones. We can use one natural system to model another natural system.

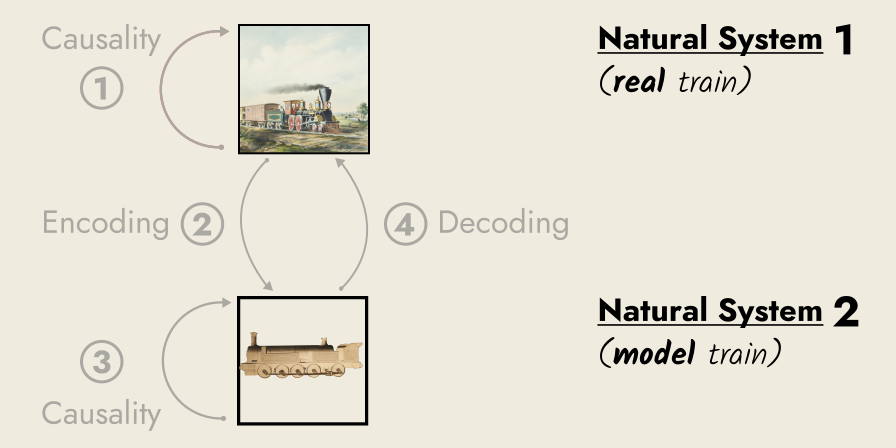
Engineers call this technique “scale modeling”, and use it to design airplanes, submarines, and everything in between. They learn about one system by studying another—since, for some aspects, the two natural systems can be brought into a modeling relation.

We can even use one formal system to model another formal system. The field of analytical geometry (aka Cartesian geometry) involves the use of algebra, a formal system, to study the properties of geometric objects—objects in another formal system.

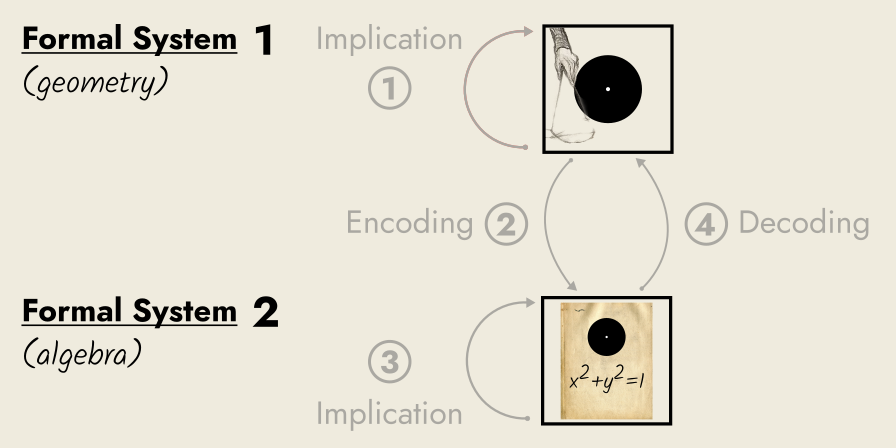
The ancient Greeks were brilliant geometers, but they had no notion of things like the “equation of a circle”, as we do now. Nowadays, we can use algebra to model geometric shapes, allowing us to quickly calculate their area etc.

Robert Rosen’s concept of the “modeling relation” represents the most powerful tool for characterizing science, mathematics and their relationship to the real world. It subsumes the entire scientific enterprise, providing a means to understand the activities of scientists and mathematicians, and explains the otherwise mysterious power of mathematical symbols to predict events in the real world.∎