What is Reduction?

SUMMARY:

The word “reduct” is of Latin origin and originally meant “to take or refer (a thing) to its origin”.

Reduction is an act-of-mind, where we take some abstraction (i.e. a concept, an idea), and trace it back to its originating source in the physical world.

We reduct an abstraction to understand where it originally came from—and in doing so, we aim to build an intuitive understanding of that abstraction.

TOC

Reasons to Reduct

Bringing abstractions back to Earth

a disembodied man's head looks at a wooden block and forms the concept of a block in his mind

Rather than treating abstractions as if they were detached from our world, I seek to ground them, to reveal their roots in our concrete reality.

I reject scientific and mathematical Platonism: the belief that abstractions are entities of some timeless and perfect “other” realm, something totally apart from our reality.

I contend that the abstractions of science and mathematics are derived from the everyday world, either directly in the case of “first-order” abstractions, or indirectly in the case of “higher-order” abstractions.

“Reduct” versus “reduce”

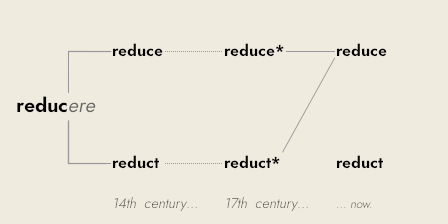
Latin word 'reducere' shown as origin for both 'reduce' and 'reduct'

Both “reduct” and “reduce” come from the Latin word reducere, which means to “lead a thing back to its origin”. They both appear in English from the 14^th century onwards.

The full history is unclear, but by the 17^th century, “reduce” came to mean “to diminish or lessen”. “Reduct” also lost its original meaning and somehow became another word for “reduce”.

I’m going to use “reduct” in its original sense of “leading a thing back to its origin”. We will “reduct” abstractions to show where they originally came from, which will “reduce” the confusion about them.

Why “reduct” an abstraction?

reduction shown as a red lightning flash tracing abstractions back to reality

An abstraction (aka a concept, idea, notion) represents the end-point of a process of abstraction, where we focus on some aspects of a thing, while ignoring others. As such, an abstraction is an object-of-the-mind and is separated from physical reality.

An example of everyday abstraction: you want to measure a length of one meter, so you use a ruler and pencil to draw such a meter-long line. The line you have drawn is an actual deposit of graphite on paper—it is a physical thing with a color, a width and a texture, but you only care about its length.

These other physical features of the line are abstracted away, ignored, allowing you to focus solely on the length (which is all you care about in this context)

Abstractions do not spring forth from nothing-at-all, and presenting them otherwise is confusing and inefficient. Abstractions are little more than formalized gibberish when introduced without their original context.

We “reduct” an abstraction to find its originating source in the real world, the world of everyday experience. Reduction is a process of “making sense” of an abstraction, by finding its starting-point in the world of the senses, where we can build an intuition for it.

The Abstraction of Area

Teaching abstractions alone is absurd

Victorian schoolmaster shouts out 'area = L squared'

Typically, scientific and mathematical topics are introduced as follows:

Teacher/textbook introduces an abstraction e.g. a formula like 𝐴 = 𝑙 × 𝑙,
Teacher/textbook provides little context on the origin of this formula,
Students perform some calculations by rote, plugging numbers into the formula.

After some mind-numbing repetition of rote calculations using the formula, the teacher/textbook assumes the abstraction is “understood”, and they move onto the next topic, to repeat the process.

Now, if this process sounds absurd in terms of achieving an “understanding” of a formula, then it’s because it is absurd.

A better way to teach abstractions

Victorian school-boys are confused by the definition of area as 'L squared'

Can we do better?

Yes, totally.

Abstractions don’t have to remain detached from reality; we can trace them back and show how they developed from real-world observations.

Rather than revealing a formula, labelling its parts and grinding out computations, we can build an understanding of the fundamental relationships expressed by the formula.

To give a concrete example of reduction, I will reduct the formula for the area of a square. Yes, this formula is simple, but within it, is contained some fundamental concepts that serve as well-spring for further insights.

Defining the area of a square, arbitrarily

Given a square (four equal sides; internal angles equal), how do we calculate its area? That is, how much surface does a given square occupy?

For me, it was pronounced by teacher/textbook that a square 𝑆, with side length 𝑙, had an area of 𝑙 × 𝑙.

That is, Area(𝑆) = 𝑙².

So a square 𝑆, has an area 𝐴, equal to its side length 𝑙, squared. I was told that this was “by definition”, but I was always left wondering at why this was so?

Where did this link between multiplication and area come from? I thought multiplication was to do with numbers, but now we’re measuring areas?

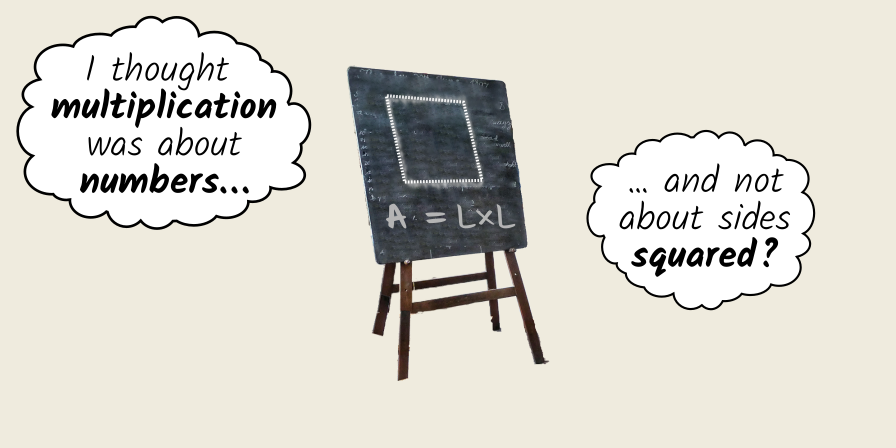
Chalkboard shows a square, with equation 'A = L × L' below

And why is area, as a concept, defined and measured in terms of square units, e.g. square meters (m²), square feet (ft²) etc.?

What is so special about squares?

And when defining these square units, the basic units of area, we define them as lengths squared. That is, we define them in terms of… themselves?

Seems to me a circular definition, no pun intended!

If the area of a square is its side length “squared”, then is the area of a triangle its side length “triangled”, and so on?

While it is easy to just “define” the area of a square to be its side length squared, it glosses over some glaring, but valid, objections.

Linking Area to Multiplication

Reducting the concept of area

Area is the amount of space enclosed within a boundary. We measure an area by comparing it to some standard unit quantitatively, i.e. we count the number of standard units contained within that space.

Since an area is two-dimensional, our unit must be two-dimensional as well i.e. a shape.

Which shape to choose as our standard unit? The square is chosen, as it has certain key properties required as a unit of area:

Tiles the plane: When fitted edge-to-edge, squares cover a surface completely, with neither gaps nor overlaps between them. This is known as “tiling the plane”. Otherwise, we will miscalculate the area due to gaps (under-estimates) and overlaps (over-estimates).
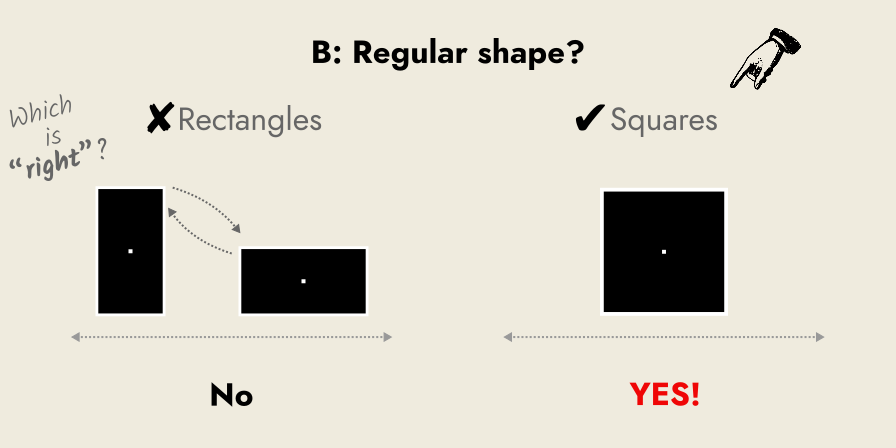
Regular shape: Squares are “regular” shapes, i.e. their sides are the same length and their internal angles are equal. There is no confusion between long/short edge, as there is with “irregular” shapes, e.g. rectangles. Squares look the same, when laid flat on any side.
Fundamental directions: On a two-dimensional surface, the fundamental dimensions are vertical (up/down) and horizontal (left/right): diagonal lines are a combination of these fundamental directions, not something by themselves. Only squares provide both fundamental directions, and only the fundamental directions.

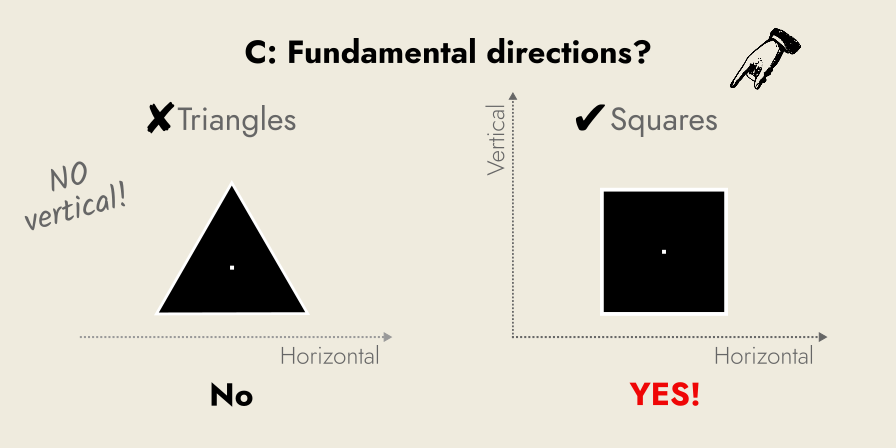
Thus, for all its inherently useful properties, the square is chosen as our fundamental unit of area (for most cases). The square becomes an abstract artifact used as the standard against which all areas are compared against.

Multiplication means multiple things

The concept of “multiplication” includes several different physical processes, among them:

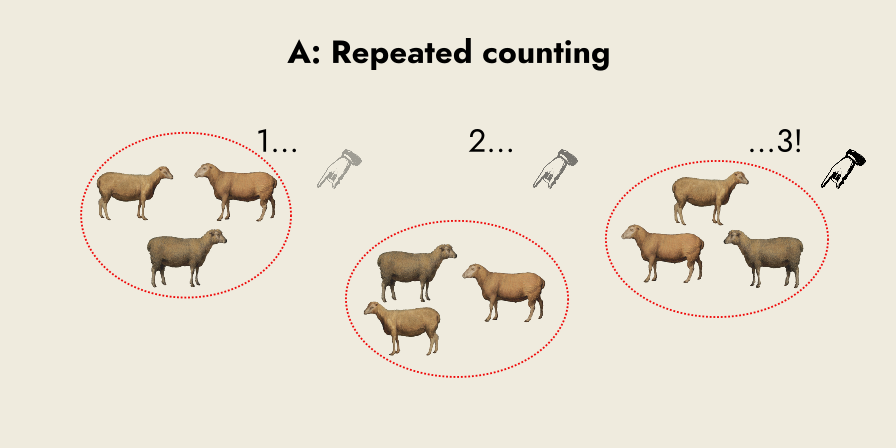
Repeated addition: adding groups of things together, rather than counting them one-at-a-time.
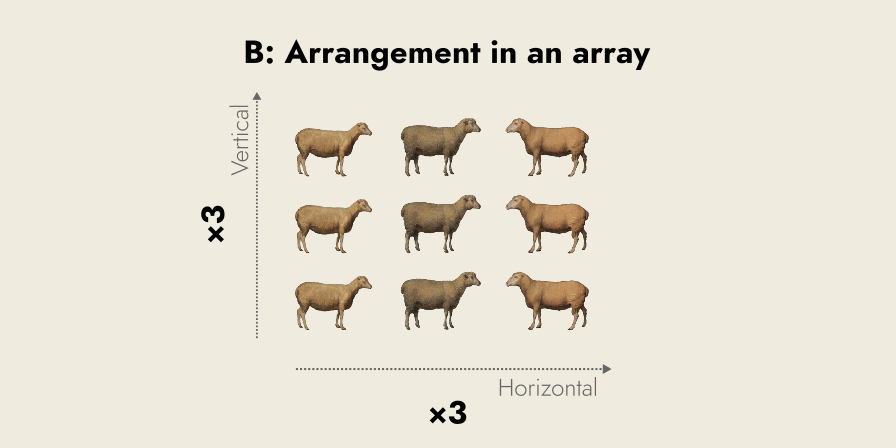
Arrangement in an array: placing things in rows (left-to-right) and columns (up-and-down), to make them easier to count. The resulting grid structure is called an array.
Scaling: altering the size of an object, e.g. making it twice as large or shrinking it down etc.

Thus the familiar multiplication sign ×, is an abstraction that can be interpreted in several different ways. Typically though, the ambiguous nature of the × symbol is not discussed, merely glossed over, leading to confusion.

Since we measure an area by counting the number of square units within that surface, and multiplication allows us to count things easily, a connection between multiplication and measurement is now developing.

“By”: Extension in another dimension

aluminum foil stretched out to form a square sheet of foil

To “square” a line means to extend that line in another dimension, to create a two-dimensional surface from a one-dimensional line. We call the resulting abstract surface a “plane”, and this plane can be tiled with square units.

Imagine taking a meter long roll of aluminum foil, and pulling out another meter length to create a surface: this is what “squaring” a line looks like, if reducted to a real-world example.

This surface represents one meter by one meter, i.e. one meter squared, m²; the numeral “2” indicates that this a two-dimensional unit, rather than a one-dimensional meter length, m.

We use the word “by”, to refer to this process of extending in a perpendicular direction—creating a surface—and we use the multiplication symbol, ×, to represent it.

Rather than the counting of distinct entities or altering the size of an object, we re-use (over-use?) the multiplication symbol to represent the creation of a surface—creating a direct link between multiplication and geometry.

Thus, having created our square unit, we can find the area of any surface, by tiling it with square units, and then multiplying to quickly count these units. The total number of these square units constitutes our measurement of area. ∎

Key Takeaways

Reduction is the “reverse” process to abstraction: we start with an abstraction (a concept) and trace it back to its origin in the physical world.
Reduction allows us to see the real-world origins of concepts, enabling us to form an intuitive understanding of them, and to understand the (otherwise) mysterious power of abstractions.
Rather than just defining area arbitrarily in terms of squares, we can reduct the equation 𝐴 = 𝑙², and see that squares have key properties that make them perfect as the fundamental unit for measuring area.
The concept of “multiplication” covers some very different physical actions, including repeated addition, scaling and the creation of a surface. These physical actions create the (otherwise) mysterious link between multiplication and geometry.