Ratio, multipart
A comparison between more than two quantities (multitudes or magnitudes) of the same type, where we compare them in terms of their relative size.
The things being compared are called the “terms” of the ratio.
Multipart ratios are written in the form “𝑎 : 𝑏 : 𝑐 …” for each of the quantities (“terms”) being compared.
Multipart ratios are also known as multi-term or multi-step ratios.
Usage of Multipart Ratios
Multipart ratios are useful for describing how a thing is made up of its parts, when there are more than two parts.
They can provide a quantitative “breakdown” of a composed thing into the parts that compose it (in terms of their relative quantity).
Multipart ratios are frequently used in recipes, to indicate the relative amount of various ingredients, and they can involve either multitudes (individual quantities) or magnitudes (continuous quantities).
Multipart ratios with multitudes
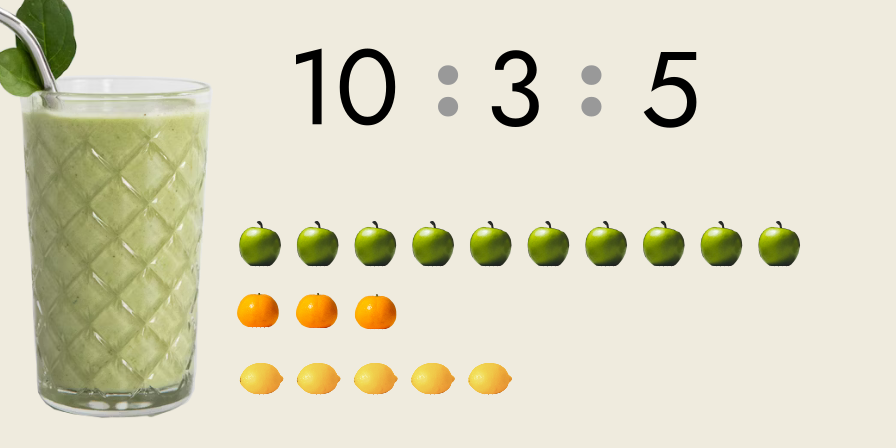
Multitudes are groups of individuals, and a simple example of a multipart ratio of multitudes is a recipe for a “smoothie”.
For a smoothie consisting of ten apples, three oranges and five lemons, you would write the multipart ratio: 10 : 3 : 5
This smoothie has a total of eighteen “parts” (18 = 10 + 3 + 5), where a “part” means a “whole fruit”:
- ten parts are apples,
- three parts are oranges, and
- five parts are lemons.
If we had twenty apples, we would need six oranges and ten lemons for a ratio of “10
Multipart ratios with magnitudes
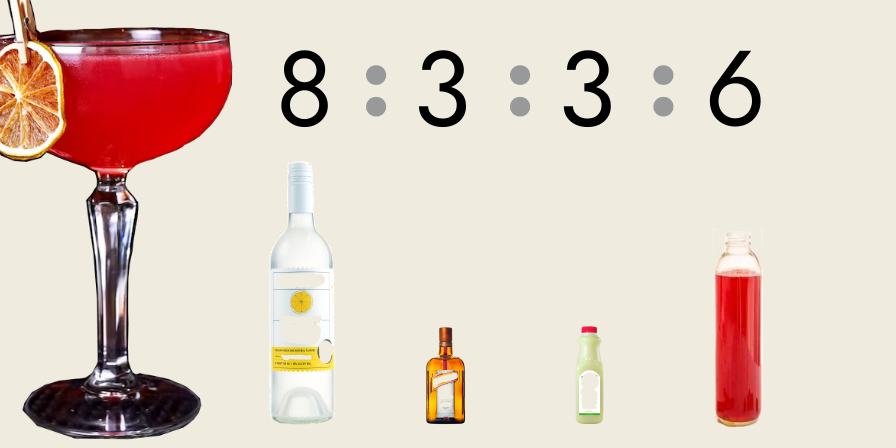
A magnitude is a continuous quantity, like distance or volume.
A recipe for a cocktail is an excellent example of a multipart ratio of magnitudes, as they involve volumes of liquids.
Consider the “cosmopolitan”, which is described by the following ratio of ingredients:*
- 40 mL lemon flavored vodka,
- 15 mL Cointreau,
- 15 mL fresh lime juice,
- 30 mL cranberry juice.
We can list the relative quantities of these ingredients, in whole numbers, as “8 : 3 : 3 : 6”.
This gives a total of twenty “parts” of the final volume, since: 8 + 3 + 3 + 6 = 20
Where all twenty parts are the same volume of liquid.
How much liquid is in each part?
Well, it depends on the final volume that we need to make.
If we need a litre of cosmopolitans, then we know that each “part” is 50 millilitres (mL), since: 1,000 mL ÷ 20 = 50 mL (1 litre = 1,000 mL)
Then, we can calculate the relative amounts of each ingredient:
- eight parts out of twenty lemon flavored vodka, which is 400 mL (8 × 50 mL).
- three parts out of twenty Cointreau, which is 150 mL (3 × 50 mL).
- three parts out of twenty fresh lime juice, which is 150 mL (3 × 50 mL).
- six parts out of twenty cranberry juice, which is 300 mL (6 × 50 mL).
And the same relations apply, whether we want to make one litre, ten litres or any other volume of cosmopolitans.
* Recipe taken from International Bartenders Association, official cosmopolitan recipe.
