Rate, multipart
A comparison between more than two quantities (multitudes or magnitudes) of a different type.
The quantities being compared are called the “terms” of the rate.
Multipart rates are also known as multi-term or multi-step rates.
Multipart rates are usually written using the forward slash, /, to separate the terms: “𝑎 units / 𝑏 units / 𝑐 units…”
As with rates, the forward slash (a.k.a. solidus ), /, is read aloud as “per”, which just means “for each”.
Usage of Multipart Rates
Multipart rates are everywhere in science—from physics to biology, and all fields in between.
Whenever you see some scientific calculation with more than two units in it, then you are dealing with a multipart rate.
Acceleration under gravity is a simple example: 9.8 metres per second per second
(Yes, two terms are seconds, relating to time, but they need to be accounted for separately.)
It is typically measured in metres (m) per second (s) per second (s).
Acceleration under gravity, in “basic” rate format, is written: 9.8 m / 1 s / 1 s
This “basic” format for rates is ideal for recording your observations.
You group terms together by how they happen in the real world, as a number and its unit, together.
However, this is not rates are written in scientific calculations.
Why? Well, it is easier if we convert these rates of terms into another format, to allow calculations to be made.
What is this other format?
“Rational number and grouped units” format.
So, starting with: 9.8 m / 1 s / 1 s
First, move the numbers from each term to the left, and calculate their result (where “per” means division): 9.8 ÷ 1 ÷ 1m / s / s
Then, you keep all units to the right, as a group: = 9.8 m / s / s keeping track of the arithmetical operations you did on the numbers, so you can convert back to physical reality.
(In this case, all we did was divide everything, so the units are written as metres/second/second.)
Multipart rates with repeated terms
Speed is the distance you travel in a given unit of time.
It is a rate of change of distance travelled per time, measured in units like miles per hour (mph), or metres per second (m/s).
Acceleration is the rate of change of your speed (either increasing or decreasing) over time.
A “rate of change” of a “rate of change”.
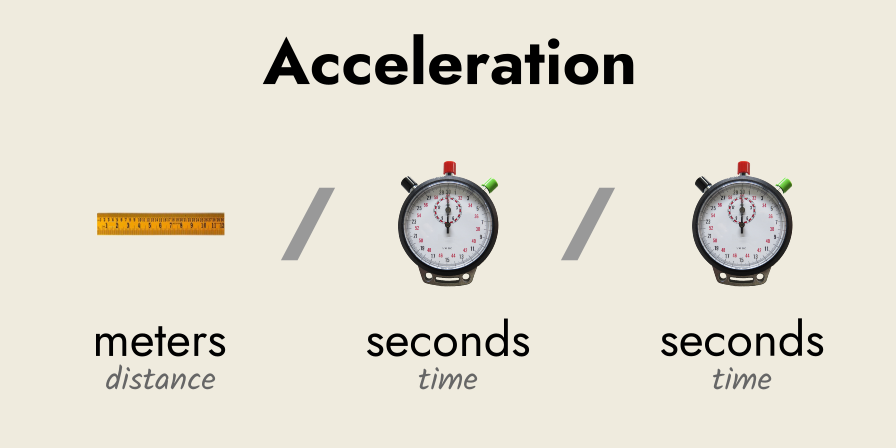
As mentioned, acceleration can be thought of as a multipart rate, one with repeated terms (the seconds): 9.8 m / 1 s / 1 s (for acceleration under gravity)
The International System of Units (SI) uses the “rational number and grouped units” format, with the multipart rate written as: = 9.8 ÷ 1 ÷ 1 m/s/s = 9.8 m/s/s = 9.8 m/s²
But, ultimately, the SI format is derived from the original “rate of terms” notation, i.e.: 9.8 m / 1 s / 1 s and I would advise keeping this original formulation in mind when thinking in rates—to avoid confusion by the jumble of units on the right-hand side of the SI format.
Multipart rates with unique terms

While acceleration has repeated terms (metres per second per second ), there are multipart rates with unique terms, i.e. no repeated terms.
One close to my own heart is “VO2 max”, a name derived from three abbreviations:
- “V” for volume,
- “O2” for oxygen, and
- “max” for maximum.
VO2 max measures cardiovascular fitness and represents the maximum rate of oxygen consumption achieved during physical effort.
It is used to test fitness in athletes, but also in a healthcare setting, to assess patient’s cardiovascular function etc.
For athletes, measuring their VO2 max is a fun experience.
They strap a mask on your mouth and nose, one hooked to a machine measuring your breathing.
Then, they stick you on a treadmill, and keep upping the speed until you cannot keep up—the point of physical collapse, basically.
(They don’t go so hard on hospital patients, for obvious reasons.)
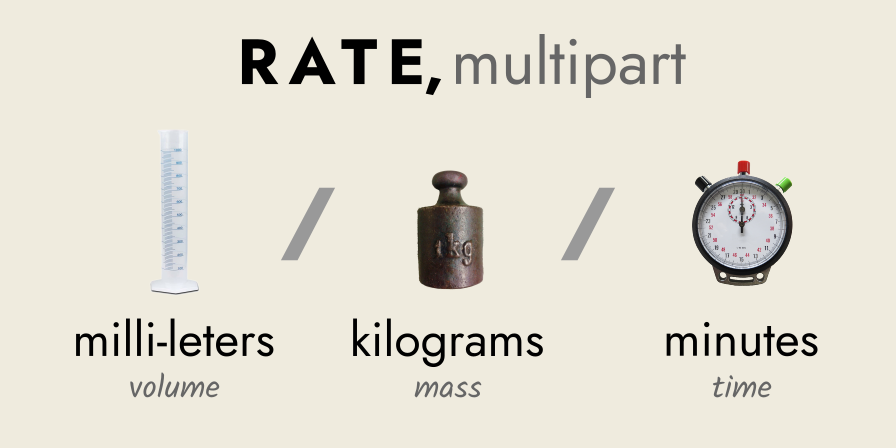
VO2 max is a multipart rate, with three completely different terms:
- milliliters (mL) of oxygen consumed per
- kilograms (kg) of body weight per
- minutes (min) of time.
For a test that took 20 minutes to exhaust an 80 kg athlete, we can record the multipart rate: 90,000 mL / 80 kg / 20 min
And, as above, we can convert this to SI format: = 90,000 ÷ 80 ÷ 20 mL/kg/min = 1,125 ÷ 20 mL/kg/min = 56.25 mL/kg/min to give a result in terms of unit values.
