Logarithm
A logarithm is a number that comes from relating numbers in a geometric sequence, to numbers in an arithmetic sequence.
The word “logarithm” was coined by John Napier from two ancient Greek words, logos and arithmos. It may be translated as “ratio number” or “reckoning number”, where “reckoning number” means a number used for calculation.[1]
Where Logarithms Come From

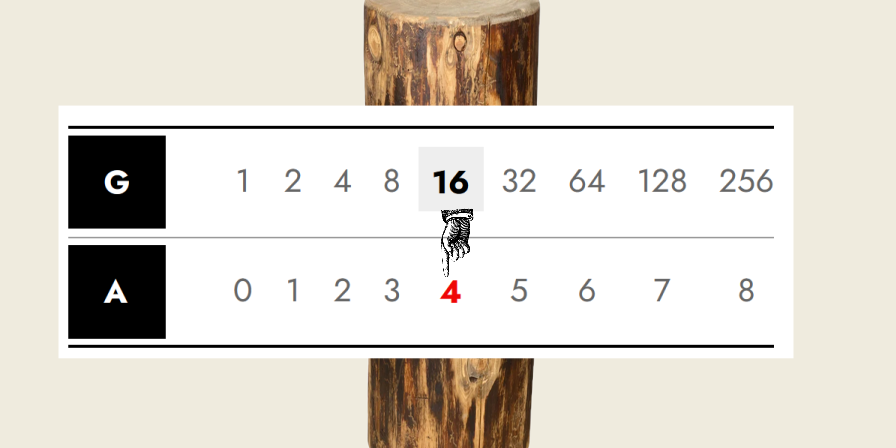
Consider a geometric sequence, G, which doubles at each term:
| G | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
|---|
Since G doubles at each term, we say G has a base of two (is “base 2”). The word “base” is just describing the ratio between the terms of this geometric sequence.
Now, consider the following arithmetic sequence, A, which increases by one unit at each term:
| A | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
Let’s align the two sequences, such that each term in G has a “match” in the other sequence, A. This allows us to “map” between them, and this mapping process is the basis of logarithms.
| G | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Now, we can “find the logarithm” of a number in G, e.g. “16”, simply by matching it with the corresponding term in A, i.e. “4”.
| G | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Formally, we say that the logarithm of sixteen, to the base two, is four, and we write it as: log2 16 = 4 Where “log” is short for “logarithm”.
Normally when we think of a number, we think of an abstract quantitative relationship between a multitude or magnitude, and a corresponding unit.
The number “12” could be the relationship between a dozen eggs (a multitude), and a single egg (used as a unit).
The number “23” could be the relationship between a length of twenty-three inches (a magnitude), and the unit inch.
In these cases, a number is the quantitative relationship between one thing (the unit) and another group or mass of things like it.
But we don’t have to limit the concept to numbers to just these types of scenarios.
Logarithms, as a concept, extend the types of things that we can describe in quantitative terms. They provide a mapping between the terms of two sequences, which preserves essential arithmetical relations.
We can use logarithms to relate one sequence of numbers to another sequence of numbers, where a “sequence” means a set of numbers that follow a specific pattern: “1, 2, 4, 8, 16, 32…” or “0, 1, 2, 3, 4, 5…” etc.
And relating geometric and arithmetic sequences underlies the great practical benefit of logarithms: simplifying multiplication and division to addition and subtraction, respectively.
Why Logarithms Matter

Logarithms allow us to reduce multiplication and division to addition and subtraction, respectively.
Addition and subtraction are easier to perform, since they require far fewer operations to be performed on the same two input numbers, when compared to multiplication and division.
Prior to the widespread availability of electronic calculators in the 1970s, calculations had generally been performed by hand.
Since multiplying and dividing large numbers with pen and paper is both time-consuming and error-prone, manual calculations represented a source of utter drudgery and error that scientists and engineers were keen to eliminate.
While mechanical calculators have existed since the 17 th century, they were (mostly) expensive desktop devices that were prone to breaking, and so were not widely available until Thomas de Colmar’s arithmometer, launched on a large scale in 1851. Regardless, these devices were rendered obsolete by the electronic calculator.
The concept of logarithms almost immediately led to the creation of a very widely used calculation tool in the 17 th century: the slide-rule. This device, which (in one form) looks like a set of rulers that can slide against each other, was the most common calculation tool of scientists and engineers, until it too was made obsolete by the electronic calculator.
Tables of logarithms, prepared in advance, were used to simplify calculations for hundreds of years. These tables provided more accuracy than the slide-rule, and so remained important in a number of applications—until they too were rendered obsolete by the electronic calculator.
Using tables of logarithms, we perform some basic look-ups and arithmetic, and then we can just “read off” the results of more complicated calculations: no time-consuming (or error prone!) multiplications or divisions required.
Logarithms achieve this remarkable feat of mathematical simplification by placing a geometric sequence in correspondence with an arithmetic sequence.
Consider the following geometric sequence, G, which doubles at each term:
| G | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
|---|
And the following arithmetic sequence, A, which increases by one at each term:
| A | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
If we want to use logarithms for calculations, we line up the two sequences like so:
| G | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Say we want to multiply two numbers from the geometric sequence, G, e.g. eight and thirty-two.
First, we find their corresponding entries in the arithmetic sequence, “3” and “5”—these numbers are the actual logarithms of eight and thirty-two, respectively.
| G | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Second, we just add the logarithms (3 and 5) together to get “8” on the arithmetic sequence, A.
| G | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Finally, we just convert back from the logarithm “8” (on the arithmetic sequence) to the corresponding entry of the geometric sequence: “256”, which is called the anti-logarithm of “8”.
You’ll notice that the anti-logarithm (“256”) is the answer to the original multiplication of eight by thirty-two!
So, we can use tables of logarithms to replace cumbersome multiplications and divisions with additions and subtractions.
Seems pretty magical, eh?
But, no—not magic, just mathematics.
Multiplying by eight can be considered as three doublings, performed one after another: 2 × 2 × 2 = 8
The “three” in this case, is the logarithm of eight, to the base two.
Similarly, multiplying by thirty-two can be considered as five doublings, performed one after another: 2 × 2 × 2 × 2 × 2 = 32
Again, the “five” in this case, is the logarithm of thirty-two, to the base two.
The combination of these two multiplications, 8 × 32, may be considered as three doublings, followed by five doublings, for a total of eight doublings: 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
In essence, the multiplications “stack” one after each other, allowing us to simply add their logarithms together, and read their result by taking the anti-logarithm from the matching arithmetic sequence.
And, while no longer used to simplify calculations, the concept of logarithms still has wide-ranging importance, underpinning these commonly used scientific scales:
- decibel (sound intensity),
- pH (levels of acidity or alkalinity),
- Richter (earthquake magnitude).
References
- Caulfield, Michael J. John Napier: His Life, His Logs, and His Bones. Available at: https://maa.org/book/export/html/116454. (Accessed: 9th April 2024). [Back]
